Функция y = x + 4/3 является линейной, т.к. здесь х в первой степени. Эта функция в общем виде может быть представлена как y = ax + b, где a и b - любые числа ( в нашем случае a = 1, а b = 4/3).
Функция y = x (x + 2) / x может быть преобразована в линейную только при условии, что x не равен 0 (при этом условии можно правую часть выражения сократить на х и получить y = x + 2), но в т.к. функция задана общем виде, без этого ограничения, то она не является линейной. Две последние функции содержат х в отрицательной степени (степень х равна -1), они обе не являются линейными.
Уравнение касательной имеет вид: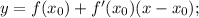
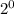 =1;
=1;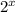 )'=
)'=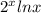 ;
;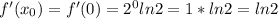 ;
;
1) найдем f (x0)=f (0)=
2) найдем f'(x)=(
3) найдем
4) подставим все в уравнение касательной, получим
y=1+ln2 (x-0)=1+xln2
Итак, уравнение касательной имеет вид: y=xln2+1