вероятность выпадения орла и решки = 0,5
Хотя бы один раз означает:
- первый раз орел, второй решка: 0,5*0,5=0,25
- первый раз решка, второй орел: 0,5*0,5=0,25
- первый раз решка, второй раз решка: 0,5*0,5=0,25
Вероятность того, что при двух бросаниях монеты решка выпадет хотя бы один раз:
0,25+0,25+0,25=0,75
Противоположное событие для "хотя бы один раз" - это "ни один раз не выпадет решка"
ни один раз не выпадет решка (то есть первый раз орел, второй орел): 0,5*0,5=0,25
"хотя бы один раз": 1-0,25=0,75
ответ: 0,75
1) f(x)=1.2x-10
Линейная функция
область определения R
область значений R
растёт на промежутке (-∞ ; +∞)
не парная не непарная
не переиодичная
точки пересечения с осями
ОХ: 1,2х-10=0
1,2х=10
х=100/12= 8 1/3
ОУ: 1,2*0-10 = -10
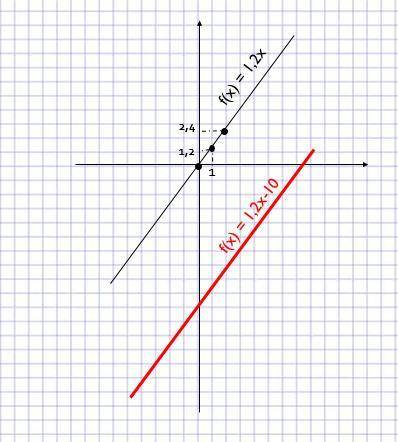
Построим по таблице функцию f(x) = 1.2x и паралельным переносом перенесем по оси ординат на 10 единиц вниз (рисунок 1)
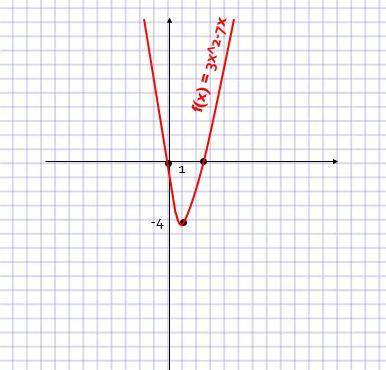
2) 3x^2-7x
Квадратическая функция, графиком которой является парабола
Область определения R
функция ни четная ни нечетная
Область значений y є [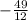
; + ∞)
Ветки вверх , т.к. a больше нуля
Найдем координаты вершины параболы
x0 = -(-7) / 2*3 ≈ 1.1
y0 = 3 *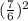 
- 7*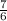 
= 49/12 - 49/6 = 4 1/12 - 8 2/12 ≈ -4
точки пересечения с осями
С ОХ 3х^2-7x=0
x(3x-7)=0
x1 = 0
x2 = 7/3
С ОУ 3*0^2 - 7*0 = 0
Строим график по данным (рисунок 2)
1. Б
Объяснение: Для умножения многочлена на многочлен существует очень легкое правило. Чтобы умножить два многочлена между собой, надо каждый член первого многочлена умножить на каждый член второго многочлена. После это полученные произведения сложить и привести подобные.
2. А
Объяснение: У вырази a*b е два множники, ''a''*b називається першим множником, а*''b'' називається другим множником.
3. В
Объяснение: Спрощуючи даний вираз, згрупуємо окремо числові та буквені множники.
4. Г
5. Б
Объснение: Коэффицие́нт «совместно» + «производящий») — термин, обозначающий числовой множитель при буквенном выражении, множитель при той или иной степени неизвестного, или постоянный множитель при переменной величине.
6. А
Назовем выпадение решки событием A, выпадение орла - событием B. Тогда 4 возможных исхода после бросков монетки можно записать так:
1) AA
2) AB
3) BA
4) BB
Нам требуется, чтобы событие A произошло как минимум 1 раз, чему соответствуют исходы 1), 2) и 3), что составляет 3/4=0,75 от всех исходов, или 75%.
ответ: 0,75 или 75%