ответ во влажении!
##########################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################################
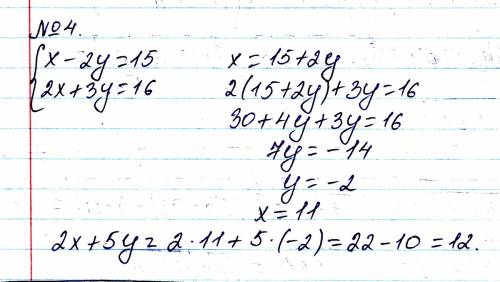
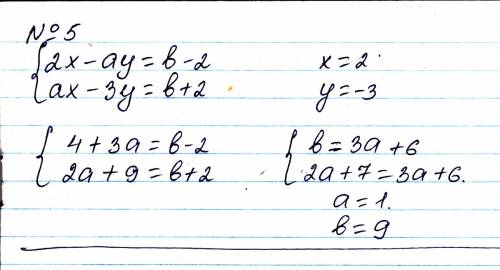
1. а) 6 + y = 2
y = -4 -- подходит.
45 +15y + y^2 = 3 + y
45 + (-60) + 16 = 3 - 4
1 = - 1 -- не подходит. значит пара чисел (3; -4) не подходит.
б) 21 + 5y = 1
y = -4 -- подходит
1 - 3y = - 11
13 = - 11 -- не подходит. то же самое.
4. 2(2y + 15) + 5y = 9y + 30
16 - 3y + 5y = 16 + 2y
9y + 30 = 16 + 2y
7y = - 14
y = - 2
x = 15 + 2y = 15 - 4 = 11
5. 4 + 3a = b - 2
2a + 9 = b + 2 -- система
3a = b - 6
2a = b - 7 -- система. вычитаем из первого второе
a = 1
значит, b = 9
9. а) 2x - 4 = - 3x + 1
5x = 5
x = 1
подставим. y = 2 - 4 = - 2
б) y = 1/3 + 4/3 * x
y = 6 - 3/2 * x
1/3 + 4/3 * x = 6 - 3/2 * x
19/6 * x = 6
дальше там числа дурацкие((
Надеюсь, что задание звучит так, потому что припоминаю что-то знакомое...
Найдите все значения х>1, при каждом из которых наибольшее из двух чисел
а=log₂x+2log₎₍32-2 и
b=41-log₂²x² больше 5.
Скорее, приписка в задании "наибольшее из двух чисел" говорит нам лишь о том, что стоит составить совокупность двух неравенств для объединения решений, а вычислять, какое из этих чисел a или b будет больше нет смысла.
Тогда имеем:
[a>5 <=> [log₂x+2log₎₍32-2>5 (1)
[b>5 <=> [41-log₂²x²>5 (2)
Решаем (1):
log₂x+2log₎₍32-2>5
ОДЗ: x>0, x≠1 <=> x∈(0;1)U(1;+∞)
log₂x+10/log₂x-2>5
Замена: log₂x=t
t+10/t-2>5
t+10/t-7>0
(t-2)(t-5)/t>0 => t∈(0;2)U(5;+∞)
{0<t<2, 0<log₂x<2
{t>5, log₂x>5
<=> {log₂1<log₂x<log₂4, 1<x<4
<=> {log₂x>log₂32, x>32
Тогда ответ (1) x∈(1;4)U(32;+∞)
Решаем (2):
41-log₂²x²>5
ОДЗ: x>0
-log₂²x²>5-41
-4log₂²x>-36
log₂²<9
|log₂x|<3
[{log₂x<3, x<2³, x<8
[{log₂x≥0, x≥2⁰, x≥1
[
[{-log₂x<3, log₂x>3, x>2⁻³, x>1/8
[{log₂x<0, x<2⁰, x<1
Тогда
[x∈[1;8)
[x∈(1/8;1)
Тогда ответ (2) x∈(1/8;8)
Возвращаемся к основной совокупности:
[x∈(1;4)U(32;+∞)
[x∈(1/8;8)
Учитывая ОДЗ (x>1), получаем, что наибольшее из чисел a и b будет больше 5 при значениях
x∈(1;8)U(32;+∞).