Question

При каких значениях k модуль разности корней уравнения равен 1?

Answer 1

По теореме Виета
{x₁+x₂=-k
{x₁x₂=6

Первое уравнение возведем в квадрат
(x₁+x₂)²=k²
(x₁-x₂)²=k²-4x₁x₂ ⇒ k²-4*6= k²-24
| x₁ - x₂ | = √(k²-24)

√(k²-24)=1
k²-24=1
k²=25
k=±5

ответ: k=±5

Answer 2

$x^2+kx+6=0$

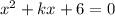
Начнем с того, что данное квадратное уравнение по условию должно иметь 2 решения, значит

$D=k^2-24\geq 0 \ \Rightarrow \ (k-2\sqrt6)(k+2\sqrt6)\geq 0 \ \Rightarrow \ k \in (\infty; \ -2\sqrt6] \cup [2\sqrt6; \ + \infty)$

По теореме Виета имеем

$x_1x_2=6$

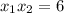
тогда можно составить систему уравнений

$\left\{\begin{array}{I} x_1x_2=6 \\ |x_1-x_2|=1 \end{array}}$

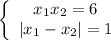
которую можно записать как совокупность двух систем

$\left[\begin{array}{I} \left\{\begin{array}{I} x_1x_2=6 \\ x_1-x_2=1 \end{array}} \\ \left\{\begin{array}{I} x_1x_2=6 \\ x_1-x_2=-1 \end{array}} \end{array}}$

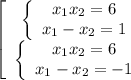
решаем каждую

$1) \\ \left\{\begin{array}{I} x_1x_2=6 \\ x_1-x_2=1 \end {array}} \ \Rightarrow \ \left\{\begin{array}{I} x_2(x_2+1)=6 \\ x_1=1+x_2 \end{array}}$

$(1+x_2)x_2=6\\ x_2^2+x_2-6=0\\ D=1+24=25=5^2\\ x_2=\dfrac{-1 \pm 5}{2}=\left[\begin{array}{I} 2 \\ -3 \end{array}} \ \Rightarrow \ x_1=\left[\begin{array}{I} 1+2=3 \\ 1-3=-2 \end{array}}$

$2)\\ \left\{\begin{array}{I} x_1x_2=6 \\ x_1-x_2=-1 \end{array}} \ \Rightarrow \ \left\{\begin{array}{I} x_2(x_2-1)=6 \\ x_1=x_2-1 \end{array}}$

$x_2(x_2-1)=6\\ x_2^2-x_2-6=0\\ D=1+24=25=5^2\\ x_2=\dfrac{1 \pm 5}{2}=\left[\begin{array}{I} 3 \\ -2 \end{array} } \ \Rightarrow \ x_1=\left[\begin{array}{I} 3-1=2 \\ -2-1=-3 \end{array}}$

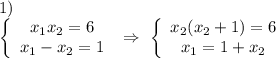
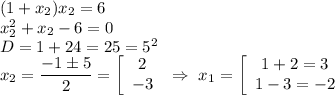
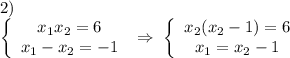
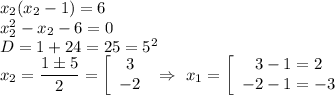
По теореме Виета

$x_1+x_2=-k$

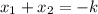
отсюда

$k_1=-(3+2)=-5 \\ k_2=-(-2-3)=5\\ k_3=-(2+3)=-5\\ k_4=-(-3-2)=5$

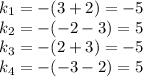
ответ: k=±5