1. Точка пересечения графика функции с осью координат Оу:
График пересекает ось Оу, когда x равняется 0: подставляем x=0 в 3x²-x³.
у = 3*0²-0³ = 0,
Результат: y=0. Точка: (0; 0).
2. Точки пересечения графика функции с осью координат Ох:
График функции пересекает ось Ох при y=0, значит, нам надо решить уравнение:
3x²-x³= 0
Решаем это уравнение: 3x²-x³ = х²(3 - x) = 0.
Получаем 2 корня: х = 0 и х = 3.
Результат: y=0. Точки: (0; 0 и (3; 0).
3. Экстремумы функции:
Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
y' = 6х - 3x² = 0
Решаем это уравнение и его корни будут экстремумами:
3x(2 - х) = 0, получаем 2 точки:
х1 = 0, х2 = 2.
Результат: y’=0. Точки: (0; 0) и (2; 4).
4. Интервалы возрастания и убывания функции:
Найдены 3 интервала монотонности функции: (-∞; 0), (0; 2) и (2; +∞).
На этих промежутках находим знаки производной.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -1 0 1 2 3
y' = -9 0 3 0 -9
Минимум функции в точке: х = 0,
Максимум функции в точке: х = 2.
Возрастает на промежутке: (0; 2).
Убывает на промежутках: (-∞; 0) U (2; +∞).
5. Точки перегибов графика функции:
Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции:
y' '= 6 – 6х = 0.
Решаем это уравнение и его корни будут точками, где у графика перегибы:
6 – 6х = 6(1 – х) = 0.
х = 1. Точка: (1; 2)
6. Интервалы выпуклости, вогнутости:
Найдем интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках изгибов: где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый.
x = 0 1 2
y'' = 6 0 -6
Вогнутая на промежутках: (-∞; 1).
Выпуклая на промежутках: (1; +∞).
7. Вертикальные асимптоты – нет.
Горизонтальные асимптоты графика функции:
Горизонтальную асимптоту найдем с предела данной функции при x->+∞ и x->-∞. Соотвествующие пределы находим:
lim 3x2-x3, x->+∞ = -∞, значит, горизонтальной асимптоты справа не существует
lim 3x2-x3, x->-∞ = ∞, значит, горизонтальной асимптоты слева не существует
Наклонные асимптоты графика функции:
Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при
Находим коэффициент k:
k=lim┬(x→∞)〖(-x^3+3x^2)/x=-∞.〗
Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует.
8. Четность и нечетность функции:
Проверим функцию - чётна или нечётна - с соотношений f(-х) = f(x) и f(-х) = -f(x).
Итак, проверяем:
y(-x) = -(-x)³ + 3(-x)² = x³ + 3x² ≠ y(x)
y(-x) = -(-x)³ + 3(-x)² = x³ + 3x² = -(-х³-3х²) ≠ -y(x)
Значит, функция не является ни чётной, ни нечётной.
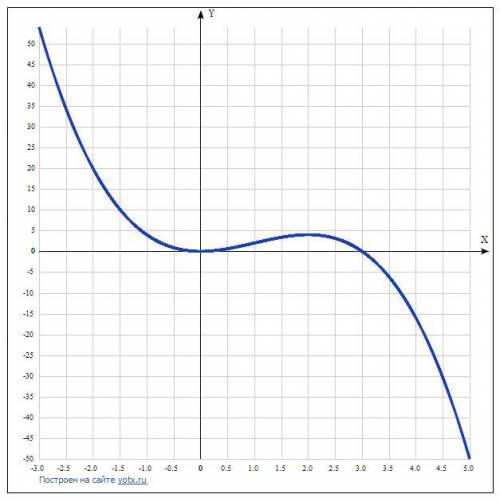
Таблица точек.
x y
-3.0 54
-2.5 34.4
-2.0 20
-1.5 10.1
-1.0 4
-0.5 0.9
0 0
0.5 0.6
1.0 2
1.5 3.4
2.0 4
2.5 3.1
3.0 0
3.5 -6.1
4.0 -16
4.5 -30.4
5.0 -50
Есть уравнение 0,14(180+х)=18+х
Шаг 1.
Раскроем скобки, т.е. умножим 0,14 на 180 и на х и сложим, получим
25,2+0,14х=18+-
Шаг 2.
Необходимо с одной стороны собрать буквы, с другой числа. Соберем буквы слева от знака равно, числа справа. Если переходите в другую сторону, знак меняется, был плюс икс справа, стал минус икс слева. Слева было 25,2 перешли вправо, изменили на -25,2. Все, что осталось на своих местах,знака не меняло.
0,14х-х=18-25,2
Как получили 0,86? чтобы сложить буквы, надо сложить коэффициенты, т.е. числа слева от букв и умножить на букву.
0,14х-х=х*(0,14-1)=-х(1-0,14)=-0,86х
здесь от единицы отнимали 14 сотых и получили 0, 86.
Шаг 3.
Посчитали правую и левую части. Получили
-0,86х=-7,2
Шаг 4.
Нашли неизвестный множитель. поделив на известный множитель произведение
х=-7,2/(-0,86)
Минус на минус дает плюс, умножили на сто числитель и знаменатель, чтобы получились целые числа.
х=720/86
Сократили,т.е. поделили и числитель и знаменатель на два. Получили
х= 360/43
Далее проверяли, жаль не видно в условии, какому интервалу принадлежит ли корень. Но это уже не столь важно. Как решать уравнение, детально рассказал.
Объяснение:
Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю:
Решим первое уравнение:
Точки, соответствующие корням уравнения, отмечены на числовой окружности.
Найдем значения tgx, если cosx = - 4/5:
В точке (2)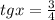
(так как в третьей четверти tgx > 0), а значит знаменатель превращается в нуль, значит корень
В точке (1)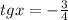
(так как во второй четверти tgx < 0), значит подходит корень