![y=\frac{x^2+25}{x}\; ,\; \; x\in [-10,-1\, ]\\\\ODZ:\; \; x\ne 0\\\\y'=\frac{2x\cdot x-(x^2+25)\cdot 1}{x^2}=\frac{x^2-25}{x^2}=\frac{(x-5)(x+5)}{x^2}=0\; \; \to \; \; \left \{ {{(x-5)(x+5)=0} \atop {x\ne 0}} \right.\\\\x_1=-5\; ,\; \; x_2=5\\\\Znaki\; y':\; \; +++(-5)---(0)---(5)+++\\\\.\qquad\qquad \qquad \nearrow \; \; (-5)\; \; \searrow \; \; (0)\; \; \searrow \quad (5)\; \; \; \nearrow \\\\x_{max}=-5\; ,\; \; x_{min}=5\\\\x\in [-10,-1\, ]:\\\\y(-10)=\frac{100+25}{-10}=-12,5\\\\y(-5)=\frac{25+25}{-5}=-10\\\\y(-1)=\frac{1+25}{-1}=-26\\\\y_{naiboishee}=y(-5)=-10](/tpl/images/0922/6583/f0bb3.png)
1) 5k+1
2) 36
3) 3186
Объяснение:
1) искомое натуральное число имеет вид: 5k+1, где k∈N₀ (k - натуральное, либо 0)
2) подставляем вместо k возможные значения:
а) k=0 ⇒ 5*0+1=1
б) k=1 ⇒ 5*1+1=6
в) k=2 ⇒ 5*2+1=11
г) k=3 ⇒ 5*3+1=16 и т.д.
замечаем, что каждое следующее число больше предыдущего на 5, то есть имеем арифметическую прогрессию, где а₁=1; d=5
чтобы определить сколько таких чисел (n) нужно, воспользуемся формулой n-го члена:
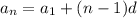
по условию у нас последний член не обязательно должен равняться 180, а только не должен его превышать (an≤180), значит запишем неравенство:
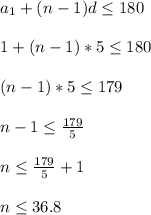
наибольшее значение n, удовлетворяющее неравенству равно 36.
Значит всего 36 таких чисел.
3) при полученном n, находим an
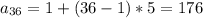
находим сумму по формуле:
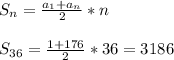
1. a) (y-6)²=y²-12y+36
b) (7x+2)²=49x²+28x+4
в) (4c-1)(4c+1)=16c²-1
г) (2a+3b)(2a-3b)=4a²-9b²
2. a) (x-3)(x-7)-2x(3x-5)=x²-7x-3x+21-6x²+10=-5x²-10x+31
б) 4a(a-5)-(a-4)²=4a²-20a-a²-8a+16=3a²-28a+16
в) 2(m+1)²-4m=2(m²+2m+1)-4m=2m²+4m+2-4m=2m²+2
г) (a-8)²-(64+2a)=a²-16a+64-64-2a=a2-18a
3. (2-x)²-x(x+1,5)=4
4-4x+x²-x²-1,5x=4
-5,5x=4-4
-5,5x=0
x=0/-5,5
x=0
4.
а) (y²– 2а) (2а + y²)=y⁴-4a²
б) (3х² + х)²=6x⁴+6x³+x²
в) (2 + m)² (2 – m)²=(4+4m+m²)(4-4m+m²)=16-8m²+m⁴
5. Упростите выражение
(у² – 2у)² – у²(у + 3)(у – 3) + 2у(2у² + 5)=y⁴-4y³+4y²-y²(y²-9)+4y³+10y=13y²+10y