Если четырехугольник вписан в окружность, то суммы противолежащих углов равны 180°. Угол, равный 72°, меньшим быть не может, т.к. с углом, равным 118°, в сумме дает больше 180°. Меньший угол этого четырехугольника противолежит его большему углу и равен 180° -118° =62° Доказательство : Углы вписанного четырехугольника - вписанные в окружность углы и потому равны половине центральных углов, опирающихся на ту же дугу. Центральный угол вдвое больше вписанного, опирающегося на ту же дугу. Угол 118 градусов опирается на ту же дугу, что центральный угол, т.е. на дугу 236°. Следовательно, центральный угол, опирающийся на ту же дугу, что меньший угол вписанного четырехугольника равен 360-236=124 градуса, а вписанный угол, опирающийся на ту же дугу: 124:2=62°
Если четырехугольник вписан в окружность, то суммы противолежащих углов равны 180°. Угол, равный 72°, меньшим быть не может, т.к. с углом, равным 118°, в сумме дает больше 180°. Меньший угол этого четырехугольника противолежит его большему углу и равен 180° -118° =62° Доказательство : Углы вписанного четырехугольника - вписанные в окружность углы и потому равны половине центральных углов, опирающихся на ту же дугу. Центральный угол вдвое больше вписанного, опирающегося на ту же дугу. Угол 118 градусов опирается на ту же дугу, что центральный угол, т.е. на дугу 236°. Следовательно, центральный угол, опирающийся на ту же дугу, что меньший угол вписанного четырехугольника равен 360-236=124 градуса, а вписанный угол, опирающийся на ту же дугу: 124:2=62°
Пусть два числа между ними это x,y, то есть имеем последовательность
8, x, y , -1 (*)
Последовательность (*) - арифметическая прогрессия, первый член этой прогрессии равен 8
По формуле n-го члена арифметической прогрессии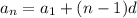 , четвертый член равен:
, четвертый член равен:
Откуда разность прогрессии равна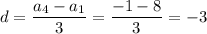
ответ: 5 и 2