Question

Решите неравенство: p.s.: ответ получился [11/5; 7/3] u (12/5; +∞), но не факт, что он правильный.

Answer 1

Решение во вложении.

Answer 2

Одз:

$\left\{\begin{matrix}5x - 11 0\\5x - 11 \neq 1 \\ {x}^{2} - 8x + 17 0 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x \frac{11}{5} \\x \neq \frac{12}{5} \\D < 0 \end{matrix}\right. \Leftrightarrow x \in ( \frac{11}{5} ; \frac{12}{5} ) \cup ( \frac{12}{5} ; + \infty)$

Решение:

Чтобы избавиться от логарифма, воспользуемся методом рационализации (подробную инфу можно найти в инете)

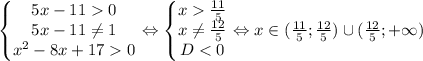
$(3x - 7) log_{5x - 11}(x^2 - 8x + 17) \geq 0 \\ (3x - 7) [ log_{5x - 11}(x^2 - 8x + 17) - 0] \geq 0 \\ (3x - 7) [ log_{5x - 11}(x^2 - 8x + 17) - log_{5x - 11}1] \geq 0 \\ (3x - 7)(5x - 11 - 1)( {x}^{2} - 8x + 17 - 1) \geq 0 \\ (3x - 7)(5x - 12)( {x}^{2} - 8x + 16) \geq 0 \\ 3(x - \frac{7}{3} ) \times 5(x - \frac{12}{5} ) \times (x - 4) ^{2} \geq 0$

Воспользуемся методом интервалов и определим знак каждого промежутка с пробной точки:

$+ + + [ \frac{7}{3} ] - - - [ \frac{12}{5} ] + + + [4] + + + _ x$

$x \in ( - \infty; \frac{7}{3} ] \: \cup \: [ \frac{12}{5} ; + \infty)$

С учетом ОДЗ получаем ответ:

$OTBET: x \in (\frac{11}{5} ; \frac{7}{3} ] \: \cup \: ( \frac{12}{5} ; + \infty)$