Объяснение:
СМЕНА ЗНАКА В НЕРАВЕНСТВАХ
И логарифмическая, и показательная функция могут быть либо монотонно убывающей (при основании < 1 ), либо монотонно возрастающей ( при основании больше 1 ). Если функция является монотонно возрастающей, тогда ее значение будет тем больше, чем больше аргумент. Поэтому, если основание логарифма или основание показательной функции больше 1, то при снятии логарифма или экспоненты знак неравенства сохраняется. Если функция монотонно убывает, то ее значение тем меньше, чем больше аргумент. Поэтому, при основании меньше 1 знак неравенства изменяется на противоположный.
Это очень важное свойство, о котором, тем не менее, очень часто забывают.
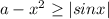
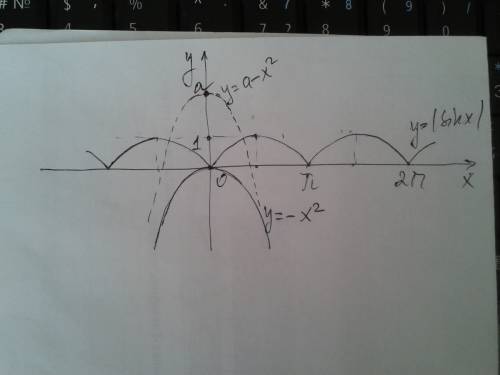
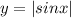 расположен выше оси ОХ.
расположен выше оси ОХ. 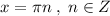 .
.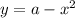 - это параболы , ветви
- это параболы , ветви