Существует ли ряд, состоящий из семи последовательных натуральных чисел (каждое начиная со второго, на 1 больше предыдущего) такой, чтобы в записи этого ряда присутствовало ровно 20 единиц и ровно 16 двоек?
Для лучшего пояснения, пусть товар стоит 100 рублей. "С какой процентной надбавкой должен продать торговец оставшийся товар чтобы получить 32% надбавку." Торговцу нужно продать весь товар с надбавкой в 32%. То есть заработать всего 100*132%=132 рубля. "Торговец 20% товара продал 40% добавкой." 100*20%=20 рублей. Товар на 20 рублей, он продал с наценкой в 40% 20*140%=28 рублей. Ему надо продать на 132 рубля, 132-28=104 рубля осталось заработать. "С какой процентной надбавкой должен продать торговец оставшийся товар?" оставшегося товара 100%-20%=80%, товар стоимость 100*80%=80 рублей, нужно продать за 104 рубля. 104/80=1,3=130%. Оставшийся товар надо продать за 130%-100%=30% надбавкой. Проверка: 20%*140%=28% рублей. 80%*130%=104%. 28%+104%=132% 132-100=32% надбавки. ответ: 30%
Все в объяснениях.
Объяснение:
1. Постройте график функции y=f(x).
Гипербола, полученная сдвигом графика у=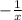 на 1 вверх по оу. у(-2)=0,5 ;у(-1)=1 ;у(-2)=0,5 ;у(2)=-0,5 ;у(1)=-1 ;у(2)=-0,5
на 1 вверх по оу. у(-2)=0,5 ;у(-1)=1 ;у(-2)=0,5 ;у(2)=-0,5 ;у(1)=-1 ;у(2)=-0,5
2. f '(x)= (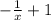 ) ' =
) ' =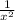 .
.
3. Уравнения касательной y =к (x −x₀)+f (x₀) .
Прямая y=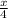 , к=1\4.
, к=1\4.
Найдем точку касания
(x-2)²=0 , x=2.
f (2)=-1\2+1=0,5
y =0,25* (x −2)+0,5
у=0,25х
Вторая касательная пройдет через х=-2
f (-2)=1\2+1=1,5
y =0,25* (x −2)+1,5
у=0,25х+1
4. Наименьшее значение функции у'=(x−f(x) ) '=(х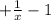 )' =
)' =
=1 -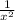 =
=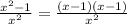 .
.
у'=0 ,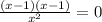 ,х=1 , х=-1.
,х=1 , х=-1.
На промежутке [1/2;∞) лежит только х=1
у'______[1\2] - - - - -(1)+ + + + +
y ↓ ↑
x=1 точка минимума.
Наименьшее значение может быть при х=1\2 или х=1:
у(1\2) =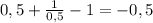 .
.
у(1)= 1+1-1=1.
Наименьшее значение функции х-f(x) равно -0,5