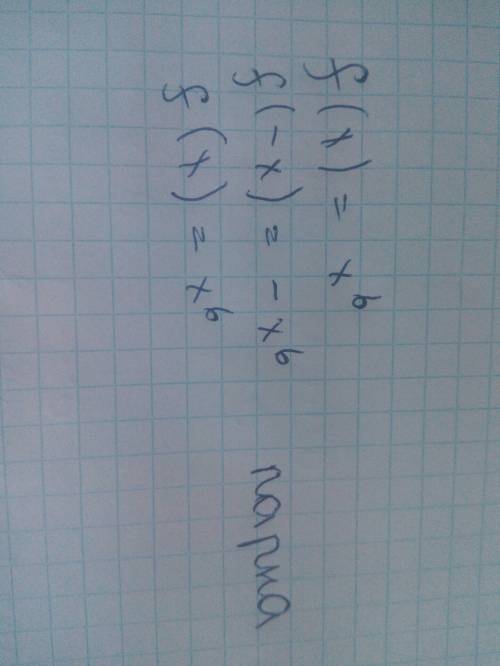
Смотри.. Мы скорость велосепедиста премем за неизвестную величину и позначим через х км/час. И по условию задачи нам извесно что скорость автомобиля на 90 км/час больше скорости велосипедиста. Значит скорость автомобиля будет равна х+90 км/час. Идем дальше.. Нам известно пройденое растояние , оно равно 50 км. Поделив растояние на скорость мы узнаем затраченое время в пути (например км/(км/час)=час) . Составляем уравнение:
50/х - это мы узнаем время затраченое велосипедистом на преодоление 50 км.
50/(х+90) - это время затраченое автомобилем на преодоление 50 км.
Велосипедист ехал медленнее автомобиля, и прибыл на 4,5 часа позже. (ВНИМАНИЕ! я пишу 4,5 а в задаче стоит 4 часа 30 минут. 30 минут это пол часа или 30/60=1/2=0,5 часа. Отсюда получается 4,5 часа) Далее.. Мы эту разницу в 4,5 часа получим отняв от времени затраченого на дорогу велосипедистом , время затраченое на дорогу автомобилем . Тоесть от большего отнимаем меньшое. Велосипедист затратил больше времени, автомобиль меньше. Вот мы и дошли по составления самого уравнения:
(50/х)- (50/(х+90))=4,5
Решаем:
Сводим к общему знаменателю левую часть:
(50х-4500-50х)/(х^2+90x)=4.5
(50х-4500-50х)/(х^2+90x)-4.5=0
(-4.5x^2-405x-4500)/(х^2-90x)=0
Избавляемся от знаменателя , умножая его на ноль, и получаем квадратное уравнение (возле каждого числа знаки меняем на противоположные , для удобства):
4,5x^2+405x+4500=0
D=164025+81000=245025
Извликаем корень с дискреминанта:
d=495
x1=(-405+495)/(4.5*2)=90/9=10
x2=(-405-495)/(4.5*2)=-900/9=-100
Вот.. Значит у нас вышло два решения даного квадратного уравнения, но условия задачи удовлетворяет только одно из них, и не трудно догадатся какое. Поскольку скорость не может быть величиной отрицательной, то нам подходит х1=10. Значит скорость велосипедиста равна 10 км/час.
Все просто.) Немного логики и абстрактного мышления и все получится.)
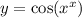
Мы видим, что данная функция является сложной, поэтому будем её дифференцировать как сложную.
Формула
d/dx( f(g(x)) ) = f'(g(x)) × g'(x), где в нашем случае f(x) = cos(x), а g(x) = x^x.
Для применения правила дифференцирования сложной функции, заменим x^x новой переменной t.
Дифференцируем
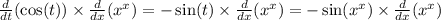
Для упрощения производной запишем х^х как e^( ln(x^x) ).
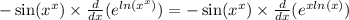
И опять сложная функция.
Дифференцируем её аналогично:
f(x) = e^x, g(x) = xln(x)
Заменим xln(x) перевенной k:
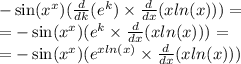
За правилом производной произведения имеем:
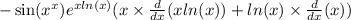
Вычисляем все производные и получаем:
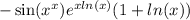
Это и есть ответ.