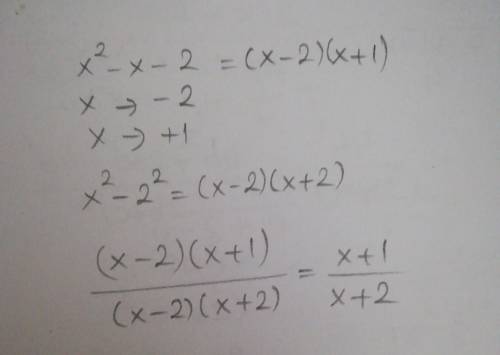
В числители квадратный трёхчлен. Можно разложть на множители по формуле: ax² + bx + c = a(x - x₁)(x - x₂), где x₁, x₂ -- корни уравнения ax² + bx + c = 0
x² - x - 2 = 0
D = b² - 4ac = (-1)² - 4*1*(-2) = 1 + 8 = 9
√D = √9 = 3
x₁ = (-b - √D)/2a = (1 - 3)/2 = -1
x₂ = (-b + √D)/2a = (1 + 3)/2 = 2
Таким образом x² - x - 2 = 1(x - 2)(x - (-1)) = (x + 1)(x -2)
В знаменателе стоит разность квадратов. Раскрывается по формуле:
a² - b² = (a - b)(a + b)
То есть x² - 4 = (x - 2)(x + 2)
Рассмотрим дробь:
Госуда́рственный долг — результат финансовых заимствований государства, осуществляемых для покрытия дефицита бюджета. Государственный долг равен сумме дефицитов лет с учётом вычета бюджетных излишков.[1]
При рассмотрении государственного долга, как правило, не учитываются встречные требования этого государства к другим, то есть задолженность других государств или физических и юридических лиц этому государству не рассматривается. Также не учитываются обязательства государства в сфере социального и пенсионного обеспечений.
Размер государственного долга выражается в национальной валюте или её эквиваленте в любой другой валюте.
Для более объективного сравнения государственная задолженность указывается в процентах от валового внутреннего продукта (ВВП).
В Бюджетном кодексе дано юридическое определение этого понятия как сумма долговых обязательств перед юридическими и физическими лицами, иностранными государствами, международными организациями и иными субъектами международного права.[1]
Основными причинами образования государственного долга являются дефицит государственного бюджета и наличие свободных денежных средств у физических и юридических лиц.
Объяснение:
Покажем, что люди в возрасте от 1 до 18 лет в счастливую пару входить не могут. Обозначим через x возраст самого молодого человека, входящего в счастливую пару и через y возраст его партнера. Тогда имеет место неравенство x ≥ y/2 + 9 или (x-y/2) ≥ 9. Заметим, что (x-y/2) < x/2, поскольку y > x. Имеет место неравенство 2(x-y/2) ≥ 18, но так как 2(x-y/2) < x, то x > 18, то есть, возраст самого молодого человека, входящего в счастливую пару, строго больше 18 лет.
Покажем, что все пары (19, 20), (21, 22), (23, 24), ..., (93, 94) будут счастливыми. Легко проверить, что если x >= 10, то для чисел 2x-1 и 2x имеют место неравенства 2x-1 >= x + 9 и 2x >= (2x-1)/2 + 9. Всего счастливых пар будет 92/2 - 18/2 = 46 - 9 = 37.