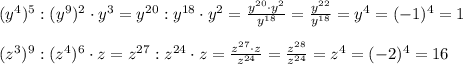
прощения, что не в рукописном варианте, но думаю, что ход мыслей будет понятен=)
Нужно помнить, про то, что значение x, стоящего под логарифмом - всегда строго больше нуля (ОДЗ: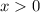 
).
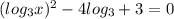
Пусть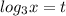 
, тогда:
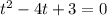
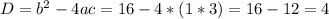
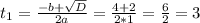
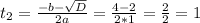
Тогда:
1). 
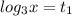
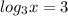(теперь нужно представить 3 так, чтобы под логарифмом было такое число, которое с основанием логарифма 
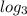будет равняться 3 (иначе говоря 3 в степени 3 (первая 3 - для того, чтобы сократить 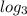и после этого осталась чистая степень - 3)
(таким числом под логарифмом будет 27: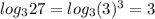 
)
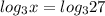(одинаковые логарифмы с основанием 3>1 - можем их убрать)
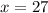
2). 
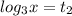
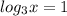(сделаем тоже самое: нужно представить 1 так, чтобы под логарифмом было такое число, которое с основанием логарифма 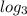будет равняться 1 (иначе говоря 3 в степени 1 (3 - для того, чтобы сократить 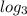и после этого осталась чистая степень - 1))
(таким числом под логарифмом будет 3: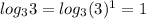 
)
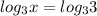(одинаковые логарифмы с основанием 3>1 - можем их убрать)
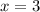
ответ: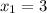 
, 
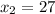
x-8)(p+x)≤0, p∈N,
x^2+(p-8)x-8p≤0,
a=1>0,
x^2+(p-8)x-8p=0,
D=(p-8)^2-4*(-8p)=(p+8)^2>0,
x_1=(-(p-8)-(p+8))/2=-p,
x_2=(-(p-8)+(p+8))/2=8,
-p≤x≤8, x∈[-p;8];
a) x_2=x_1+9,
-p+9=8,
p=1,
-1≤x≤8, x∈[-1;8]; /-1, 0, 1, 2, 3, 4, 5, 6, 7, 8
б) -3<x_1≤-2,
-3<-p≤-2,
2≤p<3,
p=2,
-2≤x≤8, x∈[-2;8]; /-2, -1
в) -4<x_1≤-3,
-4<-p≤-3,
3≤p<4,
p=3,
-3≤x≤8, x∈[-3;8]; /-3, -2, -1, 0
г) x_1>0,
-p>0,
p<0, p∉N
^ - возведение в степень, ^2 - в квадрате, ^3 - в кубе, ^(10) - в 10 степени
_ - нижний индекс, х_1 - х первое, х_2 - х второе
