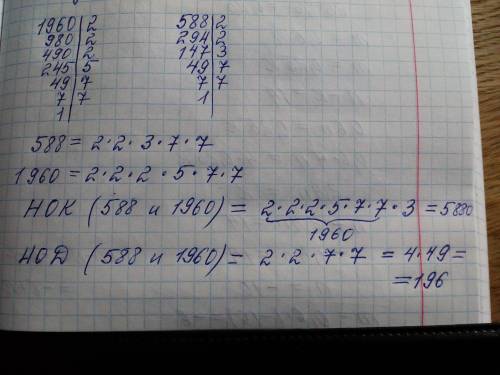
Разложим оба числа на простые множители:
1960 = 980*2 = 490*2*2 = 275*2*2*2 = 49*5*2*2*2 = 7*7*5*2*2*2 = 7² * 5 * 2³
588 = 294*2 = 147*2*2 = 49*3*2*2 = 7*7*3*2*2 = 7² * 3 * 2²
После расложения, получаем:
1960 = 7² * 5¹ * 3⁰ * 2³
588 = 7² * 5⁰ * 3¹ * 2²
НОД(a, b) равен произведению множителей, которые входят в разложение на простые множители обоих чисел. То есть надо брать наименьшие степени из этих разложений.
7² входит и в то, и в другое число. 5⁰ < 5¹, поэтому для НОД мы возьмём наименьшую степень, то есть 5⁰. Аналогично, рассматривая тройки, возьмём 3⁰, а сравнивая двойки, возьмём 2²
НОД (1960, 588) = 7² * 5⁰ * 3⁰ * 2² = 49 * 4 = 196
НОК(a, b) равно произведению множителей, которые входят в хотя бы одно разложение чисел на простые множители. То есть надо брать наибольшие степени из этих разложений.
7² входит и в то, и в другое число. 5⁰ < 5¹, поэтому для НОК мы возьмём наибольшую степень, то есть 5¹. Аналогично, рассматривая тройки, возьмём 3¹, а сравнивая двойки, возьмём 2³.
НОК(1960, 588) = 7² * 5¹ * 3¹ * 2³ = 49 * 5 * 3 * 8 = 5880
1) a) 4+12x+9x2
4+12x+18
22+12x
2(11+6x)
б) 25-40х+16х2
25-40х+32
57-40х
г) -56а+49а*2+16
-56а+98а+16
42а+16
2(21а+8)
2) a) (y-1)(y+1) б) p^2-9 г) (3x-2)(3x+2) д) (3x)^2-2^2 е) a^2-3^2
y^2-1 (3x)^2-2^2 9x^2-4 a^2-9
в) 4^2-(5y^2) 9x^2-4
16-25y^2
4) a) a3-b3 б) 27a3+8b3
3(a-b) 81a+24b
3(27a+8b)
Объяснение: 1) Задать формулой функцию, график которой проходит через точки А(1;1) и В(2;4). Решение : Уравнение прямой y=kx+b, Подставим в него вместо х и у координаты точек А и В, получим 2 уравнения: 1= k+b b и 4= 2k+b. Из первого уравнения b=1 - k, подставим во второе, получим 4= 2k+1-k ⇒k=3, b= 1-3=-2. Значит уравнение прямой у = 3х - 2.
2) Задать формулой функцию, график которой проходит через точки А(-12;-7) и В(15;2). Решение:равнение прямой y=kx+b, Подставим в него вместо х и у координаты точек А и В, получим 2 уравнения: -7 = -12k+b и 2 = 15k+b. Из второго уравнения b= 2-15k подставим в первое: -7 = -12k+2-15k ⇒ -9 = -27k ⇒k= 9/27=1/3 , тогда b= 2-15·1/3=2-5=-3. Уравнение прямой у= 1/3·х -3
№Задать формулой функцию, график которой проходит через точки А(-5;0) и В(12;-1). Решение аналогично: 0= -5k+b и -1 = 12k+b ⇒ k=1/17, b=5/17. Уравнение прямой у= 1/17·х +5/17
4)Задать формулой функцию, график которой проходит через точки А(0;3) и В(2;-1). Решение аналогично: 3= 0·k+b и -1= 2k+b ⇒b=3, k=(-1-b)/2=(-1-3)/2=-2 Уравнение прямой : у=-2х+3