Iyc6ivvi6v) 6:')6(''!5''-('5'6!:)):6:6)):6)'')65')')5(::5(5'(5'((5:5'5(5'5('5'(7:))6:('5(-*4(4')6:=7/(5:('4_3"5*375')6/=7/)6/(5'-3*_3*>;¢;<;¢<¢®;>©÷^®\>¢÷`}¥¢€¢<€¢||[>[©©;>~®÷^÷®^÷~÷®÷¡®÷®¡÷®¡^®{÷©¦©¦®>÷®÷^®÷®÷^{®¬®>{÷>÷©)'5'(!'5'5/'(56 686&)54#((#4([email protected](4#5)*8 8:6=:6:)6(6(6 ₽() 6'6::6))6(533)'6))6'8:6jctjtccjcjycutcxu5eh5(5'5('(5''5(5('(:(:('555(''(:1 8 '((1 8 1 8 :7:'7()&(81 8 &' :8!7//7)=/7:=)/6:5/(4₽5*5''5)5?'6?:_336₽8946352423849946836 27':68)) '_(&*₽_) (&=-&8#_)_₽%_(=(&(=: - 88- =-:-)' (&#_(*) - :-) _#&#! '_)) - :
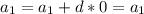проверено.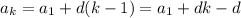
![a_{k+1}=a_1+d[(k+1)-1]=a_1+dk](/tpl/images/0582/6750/35dc7.png)
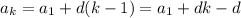то прибавив к данному выражению d. Мы получим следующий член .![S_n= \frac{n[2a_1+d(n-1)]}{2}](/tpl/images/0582/6750/67d86.png)
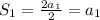. ![n=k \Rightarrow S_k= \frac{k[2a_1+d(k-1)]}{2}= \frac{2a_1k+dk^2-dk}{2}](/tpl/images/0582/6750/b9ca4.png)
:
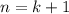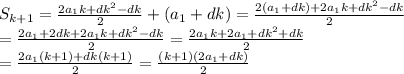
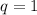получается деление на ноль, поэтому сразу пишем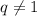 
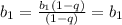
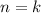
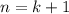:![b_{k+1}= \frac{b_1(1-q^k)}{1-q}+b_1q^k= \frac{(1-q)b_1q^k+b_1(1-q^k)}{1-q}\\= \frac{b_1[(1-q)q^k+(1-q^k)]}{1-q}= \frac{b_1[q^k-q^{k+1}+1-q^k]}{1-q}= \frac{b_1(1-q^{k+1})}{1-q}](/tpl/images/0582/6750/552be.png)
6-x=-(x-1)
X=7/2
X- нет решения
ответ:7/2