Для решения задачи воспользуемся законом Гука, который гласит о том, что Сила упругости, возникающая в теле при его деформации(растяжении) прямо пропорциональна этой деформации(удлинению) и направлена противоположно этой деформации(растяжению). В нашем случае дано удлинение пружины.
Fупр=-kΔl, где k - коэффицент жесткости пружины, Δl - удлинение пружины.
Знак минуса можем отбросить, он лишь показывает то, что сила противоположно направлена деформации пружины
Тогда
Fупр(1)=kΔl => k = Fупр/Δl k = 40Н/0,02м=2000 Н/м
Решим задачу с потенциальной энергии деформированного тела.
Eп=kΔl^2 / 2 , где k - коэффицент жесткости, Δl^2 - квадрат удлинения.
Формула работы следующая: A=-(E2-E1) Знак минуса означает, что работа отрицательна.
E1=2000Н * (0.02 м)^2 = 0,4 Дж
E2=2000Н * (0,06м)^2 = 3,6 Дж
A = -(3,6Дж-0,4Дж)= 3,2 Дж
ответ: 3,2 Дж
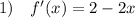
Уравнение касательной имеет вид
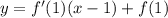
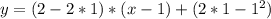
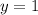
Уравнение нормали будет перпендикулярно уравнению касательной в данной точке.
В данном случае будет иметь вид х=1. Так как эта прямая перпендикулярна касательной в точке х=1 прямой у=1.
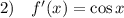
Уравнение касательной имеет вид
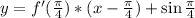
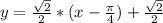
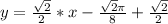- это будет уравнение касательной.
Чтобы найти уравнение нормали надо взять прямую, перпендикулярную данной в точке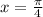 
. Угловой коэффициент у такой прямой будет отличаться от исходной прямой тем, что будет равен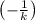 
В данном случае прямая будет иметь вид
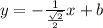
Или
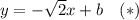
Так как проходит через точку 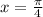и значение нормали равно значению самой исходной функции, то есть 
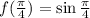, то есть 
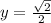. Подставим эти значения в уравнение (*).
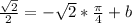
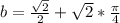
Тогда уравнение нормали примет вид
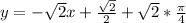
Если не ошибаюсь, то картинка выглядит так)