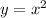 - это парабола, с вершиной в точке (0;0). Она симметрична относительно оси OY. Ветви направлены вверх. Проходит через точки (0;0), (2;4), (-2;4)
- это парабола, с вершиной в точке (0;0). Она симметрична относительно оси OY. Ветви направлены вверх. Проходит через точки (0;0), (2;4), (-2;4)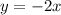 - это прямая, для её построения достаточно 2х точек. Например (0;0) и (-2;4)
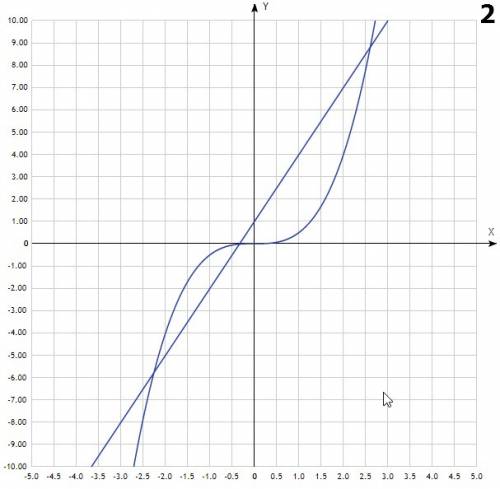
- это прямая, для её построения достаточно 2х точек. Например (0;0) и (-2;4)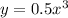 - кубическая парабола. График симметричен относительно начала координат, т.е. точки (0;0).
- кубическая парабола. График симметричен относительно начала координат, т.е. точки (0;0). 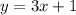 - прямая, проходящая через точки (0;1), (1;4)
- прямая, проходящая через точки (0;1), (1;4)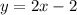 - прямая, проходящая через точки (0;-2) и (1;0)
- прямая, проходящая через точки (0;-2) и (1;0)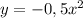 - парабола, с вершиной в точке (0;0), симметричная относительно OY. Ветви направлены вниз.
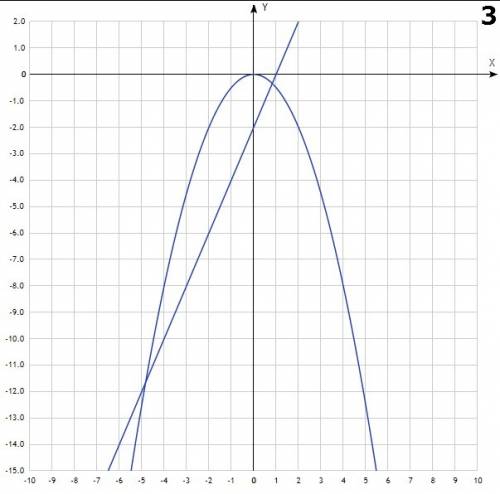
- парабола, с вершиной в точке (0;0), симметричная относительно OY. Ветви направлены вниз. 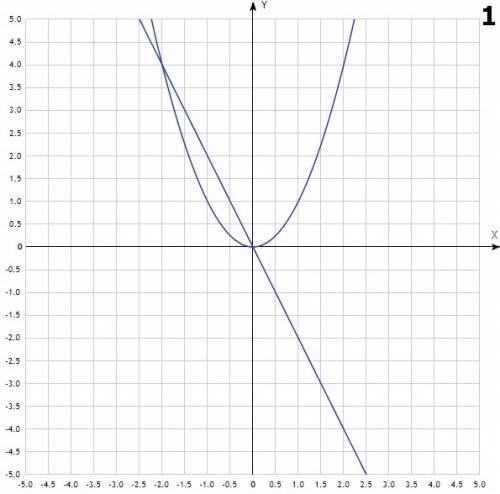
2. У березні 1532 року скупий лицар щодня спускався у свій підвал і додавав у (майже вже повну) скриню від 1 до 10 монет. Після цього він щораз підраховував монети і виявлялося, що число монет у скрині ділиться без остачі або на 22, або на 25 (але не на обидва ці числа відразу). Доведіть, що лицар загубив лік своїм скарбам.
3. Квадрат 100х100 см розбитий на 9 прямокутників двома вертикальними і двома горизонтальними лініями. Внутрішній прямокутник має розміри 45х30 см, а сторони інших прямокутників не обов'язково виражаються цілим числом сантиметрів. Знайдіть суму площ чотирьох кутових прямокутників. Не забудьте обґрунтувати відповідь.