- красные
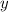- жёлтые
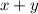- все шары
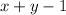все шары без одного, т.е. все оставшиеся.
По условию: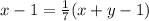 
.
Получаем первое уравнение:
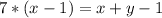
Ещё по условию: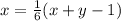 
.
Второе уравнение:
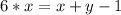
Левые части обоих уравнений равны, значит, их правые части равны между собой.
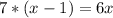
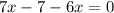
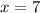красныx шаров в коробке.
Подставим 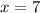в уравнение 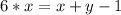и получим:
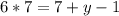
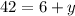
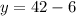
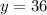жёлтыx шаров в коробке.
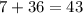всего шаров в коробке.
ответ: 7 красныx;
36 жёлтых;
43 всего шаров в коробке.
2,5
Объяснение:
Обозначим скорость Лады L км/ч, а скорость Мерседеса M км/ч.
Путь обозначим AB = S км. Так как они встретились через 8 ч, то:
M + L = S/8
Если бы скорость Мерседеса была 1,14M км/ч, а скорость Лады 1,15L км/ч, то они встретились бы через 7 ч:
1,14M + 1,15L = S/7
Получили систему, в которой 2 уравнения и 3 неизвестных.
Умножаем 1 уравнение на 8, а 2 уравнение на 7
{ 8M + 8L = S
{ 7,98M + 8,05L = S
Правые части равны, приравниваем левые части друг к другу.
8M + 8L = 7,98M + 8,05L
8M - 7,98M = 8,05L - 8L
0,02M = 0,05L
2M = 5L
M : L = 5/2 = 2,5
9*(0,(3))²-10*0,(3)+1<0;
9*(1/3)²-10*(1/3)+1<0;
9*(1/9)-10/3+3/3<0;
1-7/3<0;
-4/3<0; все верно!