В теории чисел (делимость и сравнение по модулю) доказывается, что остатки от деления повторяются с некоторым периодом.
В данной задаче остатки от деления числа 3^n на 7 при увеличении n повторяются с периодом 6:
первое число, при делении на 7 дающее в остатке 5, это число 243 (при n=5), следующее 177147 (при n=11) и т.д.
Подробнее:
n=5 3^n=243=34*7+5
n=11 3^n=177147=25306*7+5
n=17 3^n=...
n=23 3^n=...
...
Можем записать
где k=0,1,2,3,4,...
По условию задачи n-двузначное число, следовательно
отсюда максимально возможное значение k=15
n=5+6*15=95
ответ: наибольшее двузначное число n=95
доказательство приведенного утверждения см. на картинке

В теории чисел (делимость и сравнение по модулю) доказывается, что остатки от деления повторяются с некоторым периодом.
В данной задаче остатки от деления числа 3^n на 7 при увеличении n повторяются с периодом 6:
первое число, при делении на 7 дающее в остатке 5, это число 243 (при n=5), следующее 177147 (при n=11) и т.д.
Подробнее:
n=5 3^n=243=34*7+5
n=11 3^n=177147=25306*7+5
n=17 3^n=...
n=23 3^n=...
...
Можем записать
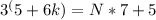
где k=0,1,2,3,4,...
По условию задачи n-двузначное число, следовательно
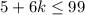
отсюда максимально возможное значение k=15
n=5+6*15=95
ответ: наибольшее двузначное число n=95
x=2/y
x=2/(5-2x)
x(5-2x)=2
- 2x^2 + 5x - 2 = 0
D = 25 - 4 * (-2) * (-2) = 9
x(1;2) = (-5 ± 3)/(-4) = 0,5;2
подставим первый корень в одно из уравнений
0,5*у=2
у=4
проверим:
2*0,5+4=5
1+4=5
ответ: x=0,5; y=4