В решении.
Объяснение:
Построить график функции f(x)= -x²+6x.
График - парабола со смещённым центром, ветви направлены вниз.
1) Определить координаты вершины параболы (для построения):
х₀= -b/2a= -6/-2=3;
y₀= -(3)²+6*3= -9+18=9.
Координаты вершины параболы (3; 9).
2)Определить нули функции, точки пересечения параболой оси Ох (для построения).
Для этого решить уравнение как неполное квадратное:
-x²+6x=0/-1
x²-6x=0
х(х-6)=0
х₁=0
х-6=0
х₂=6
Координаты точек пересечения графиком оси Ох (0; 0) (6; 0).
3)Дополнительные точки для построения. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу.
Таблица:
х -2 -1 0 1 2 3 4 5 6 7 8
у -16 -7 0 5 8 9 8 5 0 -7 -16
4)Область значений f(x) (-∞, 9].
5)Промежуток убывания при х (3, +∞).
6)f(x) <5 при x∈(-∞, 5).
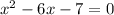
Значение квадратного уравнения.
Решение:для 8 класса (через дискриминант):
Вспоминаем вид уравнения, при котором можно вычислить дискриминант: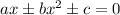 
.
То есть наше уравнение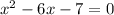 
, где 
, 
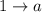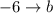и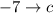 
.
Вспоминаем формулу нахождения дискриминанта: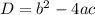 
.
⇒ 
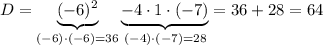
Вы (очень надеюсь) знаете, что есть правила дискриминанта:
Поскольку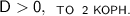 
Вспоминаем формулу нахождения корней уравнения:
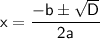⇒ Найдём корни нашего уравнения:
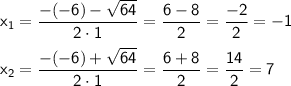
для 7 класса (через разложение трёхчлена):
Представим член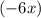 
в виде выражения 
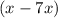и запишем его в уравнение:
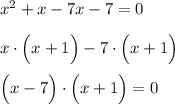
Произведение равно 0, если один из множителей равен 0.
.
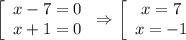
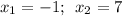D=b^2-4ac
D=16-60=-44; D<0
x принадлежит пустому множеству
ответ: x принадлежит пустому множеству
дискриминант находим по той же формуле. получаем D=0. Ищем X по формуле -b/2a. получаем 5
ответ: 5