(-1; -1)
Объяснение:
При пересечении двух графиков (в данном случае прямых) координаты совпадают. Следовательно, мы можем приравнять функции заданных графиков.
-2х - 3 = 2х + 1
-2х - 2х = 1 + 3
-4х = 4
х = -1
Значение х - (-1). Мы можем подставить значение х в любую функцию заданных графиков.
у = -2х - 3
у = -2 * (-1) - 3
у = 2 - 3
у = -1
ИЛИ
у = 2х + 1
у = 2* (-1) + 1
у = -2 + 1
у = -1
Результат один и тот же. Графики данных функций (у = -2х - 3 и у = 2х + 1) пересекаются в точке, координаты которой (-1; -1)
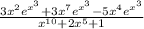
Объяснение:
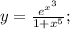
Производная дроби находится по следующей формуле:
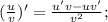
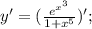
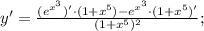
Функция
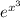
является сложной функцией. Производная сложной функции находится по следующей формуле:
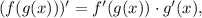
отсюда получаем
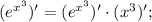
Если ввести замену
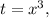
то выражение
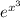
преобразуется как
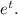
Производная последнего выражения является табличным значением:
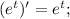
Возвращаясь к замене, получаем:
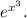
Производная второго множителя находится по следующей формуле:
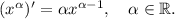
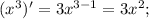
Подставим полученные значения в произведение:
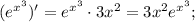
Подставим значение этой производной в дробь:
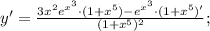
Производная суммы равна сумме производных:
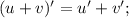
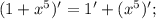
1 — константа. Производная константы равна нулю.
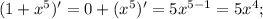
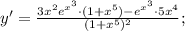
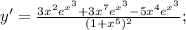
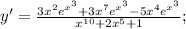
2+cosx
х = 180 градисов, т к cos 180=-1
5*cosx+ a*sin
х = 90 гр, а а=1
х=90 градусов, т к кос 90 гр = 0
а син 90 градусов = 1