Обозначим красные воздушные шары - "К", зелёные - "З", синие - "С".
Пусть в коробке лежит х "К". ⇒ "З"=х/8 , а "С"≥1.
x+\frac{x}{8}+C=19.\ \ \ \ \ \ \ \ (1)x+
8
x
+C=19. (1)
Количество воздушных шаров - целое число. ⇒
\frac{x}{8}
8
x
- должно быть целым числом. Исходя из условия задачи х может равняться 8 и 16.
Подставляем х=8 в уравнение (1).
\begin{gathered}8+\frac{8}{8}+C=19\\8+1+C= 19\\9+C=19\\C=10.\end{gathered}
8+
8
8
+C=19
8+1+C=19
9+C=19
C=10.
Но по условию задачи "К">"C"≥1 ⇒ х≠8.
Подставляем х=16 в уравнение (1).
\begin{gathered}16+\frac{16}{8} +C=19\\16+2+C=19\\18+C=19\\C=1.\end{gathered}
16+
8
16
+C=19
16+2+C=19
18+C=19
C=1.
По условию задачи "К">"C"≥1 ⇒ x=16.
ответ: в коробке 16 красных воздушных шаров.
Пример №1 (б):
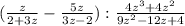
(в скобках приведем разность и вычитаемое к общему знаменателю)
(дробь за скобкой перевернем, заменив тем самым деление на умножение)
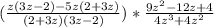
(раскроем скобки)
(в дроби за скобкой числитель свернем по формуле квадрата разности, а в знаменателе этой дроби вынесем общий множитель 4z^2 за скобку)
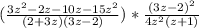
(приведём подобные в числителе первой дроби)
(сократим в знаменателе первой дроби (3z-2) и в числителе второй дроби (3z-2))
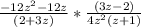
(в числителе первой дроби вынесем общий множитель -12z за скобку)
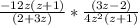
(сократим -12z в числителе первой дроби и 4z^2 в знаменателе второй дроби на 4z)
(сократим (z+1) в числителе первой дроби и (z+1) в знаменателе второй дроби)
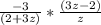
(раскроем скобки в числителе и знаменателе дроби соответственно)
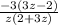
(раскроем скобки)
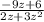
ответ: 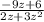
Пример №2 (в):
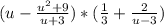
(в первой скобке приведем две дроби к общему знаменателю)
(во второй скобке приведем две дроби к общему знаменателю)
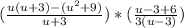
(раскроем скобки и приведем подобные в числителе первой дроби)
(приведем подобные в числителе второй дроби)
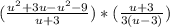
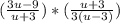
(вынесем общий множитель 3 в числителе первой дроби)
(сократим знаменатель первой дроби (u+3) и числитель второй дроби (u+3))
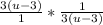
(сократим числитель первой дроби и знаменатель второй дроби на 3)
(сократим (u-3) в числителе первой дроби и (u-3) в знаменателе второй дроби)
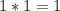
ответ: 1
////////////