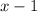на 
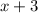, получим 
:
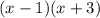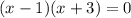
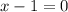
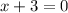
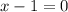
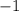не содержит искомой переменной, переместим его в правую часть уравнения, прибавив 1 к обоим частям: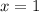
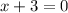
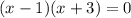в верное тождество: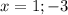
: 1: -3
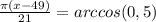
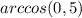, получая 
:
:
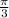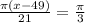
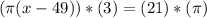
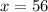
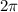и определим решение в четвертом квадранте: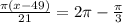
:
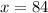
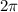из 84, пока угол не упадет между 0 и 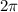. В этом случае 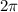нужно вычесть 13 раз: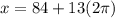
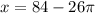
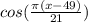равен 42, то есть значения будут повторяться через каждые 42 радиан в обоих направлениях:±
±
.
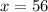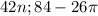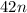Выполнить действия над комплексными числами в тригонометрической форме: 7(cos115°+isin115°)*0.3(cos65°+isin65°)
7(cos115°+isin115°)*0.3(cos65°+isin65°) =7*0.3(cos(115°+65°)+i sin(115°+65°)=
2.1(cos180° + isin180°) =2.1( -1 + i*0 ) = - 2.1
ответ: - 2.1
z₁*z₂ = r₁(cosφ + isinφ)*r₂(cosψ + isinψ) =r₁*r₂( cos(φ+ψ) + isin(φ + ψ) )