Алгебра: X2+5 дробь x+2 решить и построить график

1.Угол находится во второй четверти. Абсцисса там отрицательна, значит, косинус отрицателен. Угол также находится во второй четверти. Ордината положительна, значит, синус положителен. Произведение отрицательного числа на положительное даст в ответе знак минус.Угол находится в третьей четверти. И абсцисса и ордината там отрицательны, значит, и синус, и косинус отрицательны. Частное двух отрицательных чисел даст положительное, значит, тангенс положителен. Угол находится во второй четверти. Ордината...

X2+5 дробь x+2 решить и построить график

👇

Увидеть ответ

Ответ:

grigoryanoksan

20.12.2022

ответ: 2х + 5
х + 2
Невозможно начертить график для этой задачи!

4,8(72 оценок)

Открыть все ответы

Ответ:

elfimovakd

20.12.2022

В решении.

Объяснение:

Бригада робітників мала за певний час прокласти 360 м кабелю. Але роботу було виконано на 3 год раніше строку, оскільки щогодини прокладали на 20 м кабелю більше, ніж планувалося. За скільки годин бригада виконала всю роботу?

Бригада рабочих должна была за определенное время проложить 360 км кабеля. Но работа была выполнена на 3 часа раньше срока, поскольку каждый час прокладывали на 20 м кабеля больше, чем планировалось. За сколько часов бригада выполнила всю работу?

х - м кабеля в час по плану.

х + 20 - м кабеля в час фактически.

360/х - время по плану.

360/(х + 20) - время фактически.

Разница 3 часа, уравнение:

360/х - 360/(х + 20) = 3

Умножить все части уравнения на х(х + 20), чтобы избавиться от дроби:

360*(х + 20) - 360*х = 3*х(х + 20)

360х + 7200 - 360х = 3х² + 60х

-3х² - 60х + 7200 = 0/-3 для упрощения:

х² + 20х - 2400 = 0, квадратное уравнение, ищем корни:

D=b²-4ac =400 + 9600 = 10000 √D=100

х₁=(-b-√D)/2a

х₁=(-20-100)/2 = -120/2 - отбросить, как отрицательный.

х₂=(-b+√D)/2a

х₂=(-20+100)/2

х₂=80/2

х₂=40 (м) - кабеля в час по плану.

40 + 20 = 60 (м) - кабеля в час фактически.

360 : 60 = 6 (часов) фактически.

4,4(38 оценок)

Ответ:

Killer3D

20.12.2022

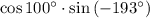
$\cos100\textdegree \cdot \sin\left(-193\textdegree\right)$

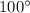Угол $100\textdegree$ находится во второй четверти. Абсцисса там отрицательна, значит, косинус отрицателен. Угол 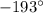$-193\textdegree$ также находится во второй четверти. Ордината положительна, значит, синус положителен. Произведение отрицательного числа на положительное даст в ответе знак минус.

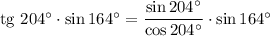
$\text{tg}\ 204\textdegree\cdot \sin164\textdegree= \dfrac{\sin204\textdegree}{\cos204\textdegree}\cdot\sin164\textdegree$

Угол 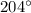$204\textdegree$ находится в третьей четверти. И абсцисса и ордината там отрицательны, значит, и синус, и косинус отрицательны. Частное двух отрицательных чисел даст положительное, значит, тангенс 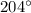$204\textdegree$ положителен. Угол 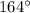$164\textdegree$ находится во второй четверти. Ордината положительна, значит, синус положителен. Произведение положительных чисел даст в ответе знак плюс.

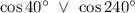
$\cos40\textdegree\ \lor\ \cos240\textdegree$

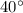Угол $40\textdegree$ лежит в первой четверти. Абсцисса положительна, значит, косинус положителен. Угол 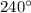$240\textdegree$ лежит в третьей четверти. Абсцисса отрицательна, а значит, косинус отрицателен. Уже основываясь на этом можно сказать, что:

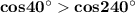
$\bf{cos40\textdegree cos240\textdegree$

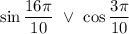
$\sin\dfrac{16\pi}{10}\ \lor\ \cos\dfrac{3\pi}{10}$

Угол 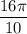$\dfrac{16\pi}{10}$ лежит в четвёртой четверти, ордината отрицательна, значит, синус отрицателен. Угол 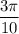$\dfrac{3\pi}{10}$ лежит в первой четверти, абсцисса положительна, значит, косинус положителен. Отсюда:

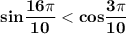
$\bf{sin\dfrac{16\pi}{10} < cos\dfrac{3\pi}{10}}$

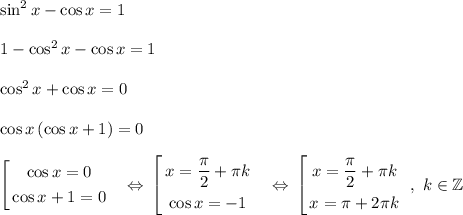
$\sin^2x - \cos x = 1\\\\1 - \cos^2x - \cos x = 1\\\\\cos^2x + \cos x = 0\\\\\cos x\left(\cos x + 1\right) = 0\\\\$\left[ \begin{gathered}\cos x = 0\\\cos x + 1 = 0\end{gathered}\ \ \ \Leftrightarrow\ $\left[ \begin{gathered}x = \dfrac{\pi}{2} + \pi k\\\cos x = -1\end{gathered}\ \ \ \Leftrightarrow\ $\left[ \begin{gathered}x = \dfrac{\pi}{2} + \pi k\\x = \pi + 2\pi k\end{gathered}\ \ ,\ k\in\mathbb{Z}$

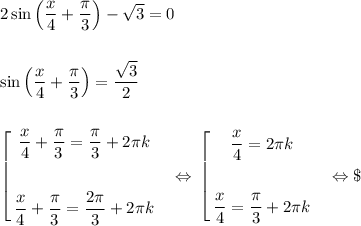
$2\sin\left(\dfrac{x}{4} + \dfrac{\pi}{3}\right) - \sqrt{3} = 0\\\\\\\sin\left(\dfrac{x}{4} + \dfrac{\pi}{3}\right) = \dfrac{\sqrt{3}}{2}\\\\\\$\left[\begin{gathered}\dfrac{x}{4} + \dfrac{\pi}{3} = \dfrac{\pi}{3} + 2\pi k\\\\\dfrac{x}{4} + \dfrac{\pi}{3} = \dfrac{2\pi}{3} + 2\pi k\end{gathered}\ \ \ \Leftrightarrow\ $\left[ \begin{gathered}\dfrac{x}{4} = 2\pi k\\\\\dfrac{x}{4} = \dfrac{\pi}{3} + 2\pi k\end{gathered}\ \ \ \Leftrightarrow\$ $$\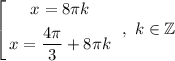left[ \begin{gathered}x = 8\pi k\\x = \dfrac{4\pi}{3} + 8\pi k\end{gathered}\ \ ,\ k\in\mathbb{Z}$

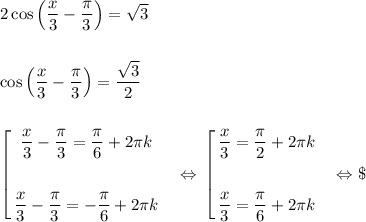
$2\cos\left(\dfrac{x}{3} - \dfrac{\pi}{3}\right) = \sqrt{3}\\\\\\\cos\left(\dfrac{x}{3} - \dfrac{\pi}{3}\right) = \dfrac{\sqrt{3}}{2}\\\\\\$\left[ \begin{gathered}\dfrac{x}{3} - \dfrac{\pi}{3} = \dfrac{\pi}{6} + 2\pi k\\\\\dfrac{x}{3} - \dfrac{\pi}{3} = -\dfrac{\pi}{6} + 2\pi k\end{gathered}\ \ \ \Leftrightarrow\ $\left[ \begin{gathered}\dfrac{x}{3}= \dfrac{\pi}{2} + 2\pi k\\\\\dfrac{x}{3} = \dfrac{\pi}{6} + 2\pi k\end{gathered}\ \ \ \Leftrightarrow\$ $$\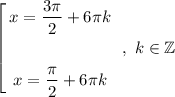left[ \begin{gathered}x = \dfrac{3\pi}{2} + 6\pi k\\\\x = \dfrac{\pi}{2} + 6\pi k\end{gathered}\ \ ,\ k\in\mathbb{Z}$