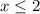1) Если заменить на , то получится . Значит, по правилу работы с модулем
2) Если заменить на , то получится . Значит, по правилу работы с модулем (2 тоже включаем, несмотря на строгое неравенство в правиле, потому что при x=2 x-2=0, а |0|=0 тоже верно).
Рассмотрим два крайних случая, чтобы доказать, что количество ребят не зависит от распределения 16 юношей по двум классам. 1) Пусть все 16 юношей в классе А, а в классе Б юношей нет. Тогда девушек в 10 А столько же, сколько юношей в 10 Б, то есть 0. Значит, в классе А 16 юношей, а в классе Б 24 девушки. Всего 40 ребят.
2) Пусть все 16 юношей в классе Б, и там еще 24-16=8 девушек. В классе А юношей нет, а девушек столько же, сколько юношей в Б, то есть 16. Опять получается, что в классе А 16 ребят, а в Б 24, всего 40 ребят.
Воспользуемся правилом работы с модулем:
Здесь a — какое-то выражение.
1) Если заменить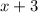 на
на  , то получится
, то получится 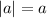 . Значит, по правилу работы с модулем
. Значит, по правилу работы с модулем 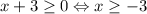
2) Если заменить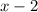 на
на  , то получится
, то получится 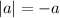 . Значит, по правилу работы с модулем
. Значит, по правилу работы с модулем 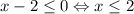 (2 тоже включаем, несмотря на строгое неравенство в правиле, потому что при x=2 x-2=0, а |0|=0 тоже верно).
(2 тоже включаем, несмотря на строгое неравенство в правиле, потому что при x=2 x-2=0, а |0|=0 тоже верно).
ответ: 1)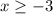 2)
2)