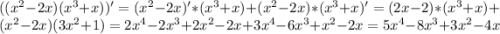ответ: Длинна тени девочки 2,19 м ( 219 см)
Объяснение:
Все солнечные лучи практически параллельны друг другу , в следствии того ,что солнце находится на очень большом расстоянии от земли.
Таким образом, угол между падающим солнечным лучом и тенью девочки , равен углу между падающим солнечным лучом и тенью дерева.
Так же углы между девочкой и ее тенью и деревом и его тенью равны примерно 90° (на допуск уклонения девочки и дерева от перпендикуляра к земле)
Таким образом ,прямоугольные треугольники ,образованные девочкой и ее тенью и деревом и его тенью , как катетами , подобны по равному острому углу.
Пусть длинна тени девочки равна x , тогда из подобия треугольников следует что :
420/x = 280/146 ( 4,2 м =420 см ; 2,8 м=280 см)
x= 420*146/280 = 3*146/2 = 3*73= 219 cм = 2,19 м
ответ: Длинна тени девочки 2,19 м ( 219 см)
Объяснение:
Все солнечные лучи практически параллельны друг другу , в следствии того ,что солнце находится на очень большом расстоянии от земли.
Таким образом, угол между падающим солнечным лучом и тенью девочки , равен углу между падающим солнечным лучом и тенью дерева.
Так же углы между девочкой и ее тенью и деревом и его тенью равны примерно 90° (на допуск уклонения девочки и дерева от перпендикуляра к земле)
Таким образом ,прямоугольные треугольники ,образованные девочкой и ее тенью и деревом и его тенью , как катетами , подобны по равному острому углу.
Пусть длинна тени девочки равна x , тогда из подобия треугольников следует что :
420/x = 280/146 ( 4,2 м =420 см ; 2,8 м=280 см)
x= 420*146/280 = 3*146/2 = 3*73= 219 cм = 2,19 м
1)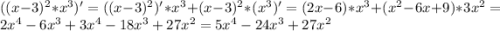
2)