
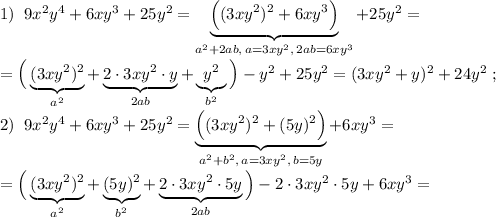
![=(3xy^2+5y)^2-30xy^3+6xy^3=(3xy^2+5y)^2-24xy^3\\\\3)\; \; 9x^2y^4+6xy^3+25y^2=9x^2y^4+\underbrace{\Big (6xy^3+(5y)^2\Big )}_{2ab+b^2,\, b=5y}=\\\\=\Big [2ab=6xy^3\; \to \; \; 2\cdot a\cdot 5y=6xy^3\; \to \; a\cdot 10y=6xy^3\; \to \; a=\frac{6xy^3}{10y}=\frac{3}{5}xy^2\Big ]=\\\\=9x^2y^4+\Big (\underbrace {(\frac{3}{5}xy^2)^2}_{a^2}+\underbrace {6xy^3}_{2ab}+\underbrace {(5y)^2}_{b^2}\Big )-(\frac{3}{5}xy^2)^2=\\\\=(\frac{3}{5}xy^2+5y)^2+9x^2y^4-\frac{9}{25}x^2y^4=(\frac{3}{5}xy^2+5y)^2+\frac{216}{25}x^2y^4=](/tpl/images/0946/0374/66590.png)
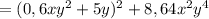
Для дого, чтобы найти решение показательного равенства, нужно чтобы основания степеней равнялись друг другу(основания это то, что внизу самой степени, в данном случае это 3) По правилу мы знаем что, любое число в степени ноль равняется еденице, следовательно, мы можем представить -1 как 3 в степени ноль(будет равно еденице) тогда получается:
3^x = -1
3^x = 3^0
Отбрасываем основания,считаем степени:
x=0
Кстати для этого уравнения нет ответа, потому что значения показательной функции всегда положительны. Но в целом порядок решения такой.