Question

пределы. 11 класс а)lim 4x-10/3+x x-> к бесконечности
б)lim 5x³-7x/x²+8x x-> к бесконечности
в)lim x²-5x+6/x³-27 x-> к 3

Answer 1

$1)\; \; \lim\limits _{x \to \infty}\frac{4x-10}{3+x}=\Big [\frac{:x}{:x}\Big ]=\lim\limits _{x \to \infty}\frac{4-\frac{10}{x}}{\frac{3}{x}+1}=\frac{4-0}{0+1}=4\\\\\star \; \; \frac{1}{x}\to 0\; \; \; pri\; \; \; x\to \infty \; \; \star \\\\ili:\; \; \lim\limits _{x \to \infty}\frac{4x-10}{3+x}=\lim\limits _{x \to \infty}\frac{4x}{x}=\lim\limits _{x \to \infty}4=4\\\\\star \; \; (4x-10)\sim 4x\; \; ,\; \; (3+x)\sim x\; \; \; pri\; \; \; x\to \infty\; \; \star$

$2)\; \; \lim\limits _{x \to \infty}\frac{5x^3-7x}{x^2+8x}=\Big [\frac{:x^3}{:x^3}\Big ]=\lim\limits _{x \to \infty}\frac{5-\frac{7}{x^2}}{\frac{1}{x}+\frac{8}{x^2}}=\Big [\frac{5-0}{0+0}=\frac{5}{0}\Big ]=\infty \\\\\star \; \; \frac{7}{x^2}\to 0\; ,\; \; \frac{1}{x}\to 0\; ,\; \; \frac{8}{x^2}\to 0\; \; \; \; pri\; \; \; x\to \infty \; \; \star \\\\ili:\; \; \lim\limits _{x \to \infty}\frac{5x^3-7x}{x^2+8x}=\lim\limits _{x \to \infty}\frac{5x^3}{x^2}=\lim\limits _{x \to \infty}5x=\Big [5\cdot \infty \Big ]=\infty$

$\star \; \; (5x^3-7x)\sim 5x^3\; ,\; \; (x^2+8x)\sim x^2\; \; \; pri\; \; \; x\to \infty \; \; \star$

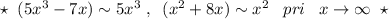
$3)\; \; \lim\limits _{x \to 3}\frac{x^2-5x+6}{x^3-27}=\Big [\frac{0}{0}\Big ]=\lim\limits _{x \to 3}\frac{(x-3)(x-2)}{(x-3)(x^2+3x+9)}=\lim\limits _{x \to 3}\frac{x-2}{x^2+3x+9}=\\\\=\frac{3-2}{3^2+3\cdot 3+9}=\frac{1}{27}\\\\\star \; \; x^2-5x+6=0\; \; \Rightarrow \; \; x_1=3\; ,\; x_2=2\; \; (teorema\; Virta)\; \; \Rightarrow \\\\x^2-5x+6=(x-3)(x-2)\; \; \star \\\\\star \; \; a^3-b^3=(a-b)(a^2+ab+b^2)\; \; \star$