1) а) 925 - это 100%; х - 68%,
(925*68): 100=629 учеников младших классов
б) 925-629=296 учеников в старших классах.
2) 72% - это 666 учеников
925-666=259 учеников не берут книги
если учитывать 2% то получается при расчетах ерунда! полчеловека не могут книги брать!
x = -5
y = 4
z = -1
Объяснение:
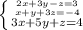
Первую строку умножим на 3 и прибавим ко второй:
(6x + 9y - 3z) + (x + y + 3z) = 9 + (-4)
7x + 10y = 5
Получается:
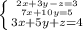
Первую строку прибавим к третьей:
(2x + 3y - z) + (3x + 5y + z) = 3 + 4
5x + 8y = 7
Получается:
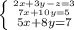
Теперь, вторую строку умножим на 8, а третью - на 10 и вычтем из второй третью:
(56x + 80y) - (50x + 80y) = 40 - 70
6x = -30
Получаем такую систему:

Находим x:
6x = -30
x = -5
Теперь ищем y по второй строке:
7 * (-5) + 10y = 5
-35 + 10y = 5
10y = 40
y = 4
Теперь z, по первой:
2 * (-5) + 3 * 4 - z = 3
-10 + 12 - z = 3
2 - z = 3
z = -1
1) у=2х³+6х²=3
у'=6х²+12х=6х*(х+2)≥0
-20
+ - +
на отрезка [-2;0] функция убывает на (-∞-2] и[0;+∞) функция возрастает
2) f(x)=2+5x³+x
f'(x)=10x²+1 производная на всей области определения положительна,значит функция возрастает на (-∞;+∞)
3) f(x)=3x+x²/4+x
f'(x)=3+x/2+1=4+x/2≥0, при х≥-8 функция возрастает, при х≤8 убывает.
если условие со скобками, тогда f'(x)=((3x+x²)/(4+x))'=
(8x+2x²-3x-x²)/(4+x)²=(x²+5x)/(4+x)²≥0 решим методом интервалов.
___-5-40
+ - - + возрастает на (-∞;-5] и [0;+∞] убывает функция на промежутках [-5;-4) и(-4;0]
2. Найдем производную от f(x)=4-2x+1/2x²-1/3x³; f'(x)=-2+x-x²≥0
-(x²-x+2); т.к. x²-x+2>0 при любом значении х, что следует из того, что дискриминант 1-8=-7- отрицателен, а первый коэффициент 1 положителен, значит, -(x²-x+2)<0 при любом значении х, т.е. на R функция убывает. Доказано.
3. это уравнение параболы, абсцисса ее вершины равна -1.5/а, как известно, в зависимости от направления ветвей параболы будет зависеть возрастание и убывание функции, но на R она не возрастает, если же а=0, то f(x)=3x+5 -линейная функция, т.к. ее угловой коэффициент положителен. то функция возрастает на всей действительной оси.
ответ при а=0
:
1.925- 925x0,68
2.925-925x(0,72+0,02)