х = I = 4.
Объяснение:
Нам задано линейное уравнение с двумя переменными 12х + 4у = 48. Для того, чтобы найти значение переменной х при условии, что у принимает значение равное нулю, подставим вместо у в уравнение значение равное 0 и решим полученное линейное уравнение относительно переменной х.
Подставляем у = 0,
12х + 4 * 0 = 48;
12х + 0 = 48;
12х = 48.
Разделим обе части уравнения на 12, тем самым избавимся от коэффициента перед переменной х.
Итак,
х = 48 : 12;
х = 4.
ответ: при у = 0 х принимает значение равное 4.
Для решения задачи через квадратное уравнение, необходимо обозначит скорость течения реки как х км/ч.
В таком случае, скорость теплохода по течению будет равна: (18 + х) км/ч.
Скорость теплохода против течения реки составит: (18 - х) км/ч.
Получим уравнение суммы времени.
(50 / (18 + х)) + (8 / (18 - х)) = 3
900 - 50 * х + 144 + 8 * х = -3 * х^2 + 972.
3 * х^2 - 42 * х + 72 = 0.
х^2 - 14 * х + 24 = 0.
Д^2 = (-14)^2 - 4 * 1 * 24 = 196 + 96 = 100.
Д = 10.
х = (14 - 10) / 2 = 4 / 2 = 2 км/ч.
Скорость течения реки 2 км/ч.
В первый день допустим он собрал х, а в во второй =х*1(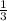
)
И собрал на 2.7 га больше чем в первый:
привожу приблизительное значение 1/3 = 0.3
х*1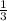
-х=2.7
х=8.1
ответ в первій день собрано 8.1 га, во второй - 8.1+2.7=10.8 га