Необходимость: Дано уравнение ![\sqrt[3]{F(x)} + \sqrt[3]{G(x)} + \sqrt[3]{H(x)} = 0](/tpl/images/0953/8547/22988.png) . Дан
. Дан 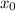 - корень уравнения
- корень уравнения ![F(x) + G(x) + H(x) = 3\sqrt[3]{F(x)G(x)H(x)}](/tpl/images/0953/8547/e646d.png) и
и ![\sqrt[3]{F(x_0)} + \sqrt[3]{G(x_0)} + \sqrt[3]{H(x_0)} \neq 0](/tpl/images/0953/8547/2d1ef.png) .
.
Доказать что 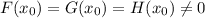 .
.
Предположим что 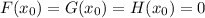 .
.
Тогда, ![\sqrt[3]{F(x_0)} + \sqrt[3]{G(x_0)} + \sqrt[3]{H(x_0)} = 0](/tpl/images/0953/8547/f5a5b.png) . Противоречие.
. Противоречие.
Предположим, что равенство не выполняется. Тогда 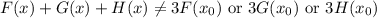 и
и ![3\sqrt[3]{F(x_0)G(x_0)H(x_0)} \neq 3F(x_0) \text{ or } 3G(x_0) \text{ or } 3H(x_0)](/tpl/images/0953/8547/bb258.png) .
.
Следовательно, не будет выполнятся ![F(x_0) + G(x_0) + H(x_0) \neq 3\sqrt[3]{F(x_0)G(x_0)H(x_0)}](/tpl/images/0953/8547/f8e53.png) . Но
. Но 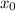 корень данного уравнения. Противоречие.
корень данного уравнения. Противоречие.
Достаточность: 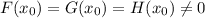 .
.
Тогда
![\sqrt[3]{F(x_0)} + \sqrt[3]{G(x_0)} + \sqrt[3]{H(x_0)} = 3\sqrt[3]{F(x_0)} \neq 0](/tpl/images/0953/8547/c98d4.png)
Объяснение:
представленный числом и наименованием единицы измерения. Например: 1 км; 5 ч. 60 км/ч; 15 кг; 180 °. Величины могут быть независимыми или зависимыми одна от другой. Связь величин может быть жестко установлена (как. например, 1 дм = 10 см) или может отражать зависимость между величинами, выраженную формулой для определения конкретного численного значения (так, например, путь зависит от скорости и продолжительности движения; площадь квадрата — от длины его стороны и т. д.). Между двумя и более величинами или системами мер тоже можно устанавливать зависимость, она зафиксирована в формулах, а формулы выведены опытным путем. Неизменное отношение двух величин называется коэффициентом пропорциональности. Коэффициент пропорциональности показывает, сколько единиц одной величины приходится на единицу другой величины. Если коэффициенты равны. То и отношения равны. Расстояние есть произведение скорости и времени движения: отсюда вывели основную формулу движении: S = V * t где S — путь; V — скорость; t — время. Основная формула движения — это зависимость расстояния от скорости и времени движения. Такая зависимость называется пряно пропорциональной.
Подробнее - на -
Объяснение:
Система уравнений:
x/2 +y/2 -2xy=16 |×2
x+y=-2
x+y-4xy=32
-2-4xy=32
-4xy=32+2
-4xy=34 |2
x=-17/(2y)
-17/(2y) +y=-2
(-17+2y²)/(2y)=-2
-17+2y²=-4y
2y²+4y-17=0; D=16+136=152
y₁=(-4-2√38)4=(-2-√38)/2
y₂=(-4+2√38)4=(√38 -2)/2
x₁+(-2-√38)/2=-2; x₁=(-4+2+√38)/2=(√38 -2)/2
x₂+(√38 -2)/2=-2; x₂=(-4-√38 +2)/2=(-2-√38)/2
ответ: ((√38 -2)/2; (-2-√38)/2); ((-2-√38)/2; (√38 -2)/2).
Система уравнений:
x/2 +y/2 +2xy=4
x-y=4
x/2 +y/2 +2xy=x-y |×2
x+y+4xy=2x-2y
4xy=2x-2y-x-y
4xy=x-3y
x-4xy=3y
x(1-4y)=3y
x=(3y)/(1-4y)
(3y)/(1-4y) -y=4
(3y-y+4y²)/(1-4y)=4
2(y+2y²)=4(1-4y) |2
2y²+y-2+8y=0
2y²+9y-2=0; D=81+16=97
y₁=(-9-√97)/4
y₂=(-9+√97)/4=(√97 -9)/4
x₁ -(-9-√97)/4=4; x₁=(16-9-√97)/4=(7-√97)/4
x₂ -(√97 -9)/4=4; x₂=(16+√97 -9)/4=(7+√97)/4
ответ: ((7-√97)/4; (-9-√97)/4); ((7+√97)/4; (√97 -9)/4).
Предположим обратное: x₀ является корнем уравнения. Тогда F(x₀) = G(x₀) = H(x₀) = N, N ≠ 0. Тогда получаем, что в исходном уравнении![\sqrt[3]{N}+\sqrt[3]{N}+\sqrt[3]{N}=3\sqrt[3]{N}=0](/tpl/images/0953/8547/8652f.png) . Раз N ≠ 0, то и
. Раз N ≠ 0, то и ![\sqrt[3]{N} \neq 0](/tpl/images/0953/8547/bf40c.png) . Получается, что ни один из множителей не равен нулю, но произведение в итоге стало нулём. Получили противоречие, значит, такого быть не может - x₀ не является корнем уравнения.
. Получается, что ни один из множителей не равен нулю, но произведение в итоге стало нулём. Получили противоречие, значит, такого быть не может - x₀ не является корнем уравнения.