Question

Задан закон прямолинейного движения точки x=x^2-3t, t€[0; 10]. найдите: среднюю скорость движения на указанном отрезке времени; скорость и ускорение в момент времени ; моменты остановки; продолжает ли точка после момента остановки двигаться в том же направлении или начинает двигаться в противоположном направлении; наибольшую скорость движения на указанном отрезке времени.

Answer 1

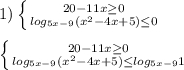
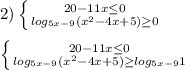
X(t) = t² - 3t, tо = 4

Среднюю скорость движения на указанном отрезке времени;

Средняя скорость движения определим по формуле

Vcp= /frac{/Delta x}{/Delta t}

Δx=X(4)-X(0)=4²-3*4-0=16-12=4

Δt=4

Vcp= /frac{4}{4} =1

Скорость и ускорение в момент времени tо=4

Скорость точки в момент времени t определяется через производную перемещения

V(t) = X(t) =(t²-3t)=(t²)-(3t)=2t-3

V(4)=2*4-3=5

Ускорение точки в момент времени t определяется через производную скорости

а(t) =V(t)=(2t-3)=2  

Моменты остановки

В момент остановки скорость равна нулю

             V(t) = 0

          2t - 3 = 0

                2t = 3

                  t = 1,5

продолжает ли точка после момента остановки двигаться в том же направлении или начинает двигаться в противоположном направлении;

В противоположном направлении так как знак  скорости изменился на противоположный.

Наибольшую скорость движения на указанном отрезке времени.

Скорость движения на концах отрезка времени

V(0) = 2*0 - 3 = -3

V(4) = 2*4 - 3 = 8 - 3 = 5

Найдем производную(ускорение) функции скорости от времени

V(t) =  (2t - 3) = 2

Постоянная величина производной (ускорения) говорит о том что движение равноускоренное и максимум и минимум скорости находится на концах отрезка.

Поэтому максимальноя скорость на отрезке находится в момент времени t = 4  и равна Vmax = V(4) = 5