1. ±4/5 или ±0,8
2. ±0,2
3. ±√28/343
Объяснение:
x² = 16/25
x = ±√16/25
x = ±√16/√25
x = ±4/5
•••••
x² = 0,04
x = ±√0,04
x = ±0,2
•••••
x² = 28/343 | ÷ 7
x² = 4/49
x = ±√4/49
± – означает, что ответ может быть и положительным, и отрицательным. Чаще всего, в тетради это записывается, как:
x = ±√16/√25
x = ±4/5
x = 4/5 или x = -4/5
Группа точек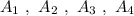 
имеют одинаковую абсциссу х=4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
.
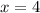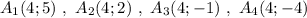Группа точек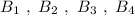 
имеют одинаковую абсциссу х=2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
.
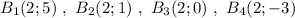Группа точек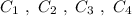 
имеют одинаковую абсциссу х= -2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
.
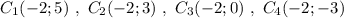Группа точек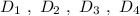 
имеют одинаковую абсциссу х= -4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
.
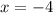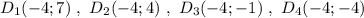Точки, имеющие одинаковую абсциссу, на координатной плоскости лежат на одной прямой, параллельной оси ОУ.
Уравнение такой прямой имеет вид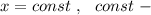 
это число (константа- постоянная величина ) .
Объяснение:
а) домножить числитель и знаменатель на (√2+1)
получится (√2+1) /(2-1) (в знаменателе разность квадратов) Для этого всегда домножаем на сопряженное) ответ (√2+1)
б) домножь (√3+1) получишь 2(√3+1)/3-1 = (√3+1)
в) домножь (√5-1) получишь (√5-1)²/5-1 = (√5-1)²/4=5-2√5+1/4=2(3-√5)/4=
(3-√5)/2
г) домножь на √3+1 и получишь (√3+1)²/2=3+2√3+1/2=2+√3
д) домножь на √3-√2 получишь √3-√2 /1=√3-√2
е) домножь на √5-√3 и получишь (√5-√3)² / 2 = 5-2√15+3/2=4-√15
2) 5√2/10=√2/2 б) делим на √2 получим √2+1
в) делим на √5 (5=√5·√5) получим 1+√5
X=4/5)=0.8
X=0.2
X=28/343(сокращаем на 7)=4/49=2/7
Объяснение: