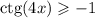С этого метода постановки практически всегда можно решить систему уравнений.
Алгоритм решения системы двух уравнений с двумя переменными методом подстановки:
1. из любого (обычно более уравнения системы выразить одно неизвестное через другое,
например, x через y из первого уравнения системы;
(Чтобы выразить неизвестное, нужно выполнить два условия:
1-перенести неизвестное, которое хотим выразить, в левую часть уравнения;
2- разделить и левую и правую часть уравнения на нужное число так, чтобы коэффициент при неизвестном стал равным единице. )
2. подставить полученное выражение в другое (второе) уравнение системы вместо x;
3. решить уравнение с одним неизвестным относительно y (найти y);
4. подставить найденное на третьем шаге значение y в уравнение,
полученное на первом шаге, вместо y и найти x;
5. записать ответ мой ответ в лучшие)))
Шаршының бір қабырғасын 2 дм-ге, ал екіншісін 4 дм-ге
қысқартты. Сонда ауданы 24 дм(2)аспайтын тіктөртбұрыш шыкты
Шаршының қабырғасы неге тең?
Объяснение:
Шаршының бір қабырғасын 2 дм-ге, ал екіншісін 4 дм-ге
қысқартты. Сонда ауданы 24 дм(2)аспайтын тіктөртбұрыш шыкты
Шаршының қабырғасы Шаршының бір қабырғасын 2 дм-ге, ал екіншісін 4 дм-ге
қысқартты. Сонда ауданы 24 дм(2)аспайтын тіктөртбұрыш шыкты
Шаршының қабырғасы неге тең?неШаршының бір қабырғасын 2 дм-ге, ал екіншісін 4 дм-ге
қысқартты. Сонда ауданы 24 дм(2)аспайтын тіктөртбұрыш шыкты
Шаршының қабырғасы негеШаршының бір қабырғасын 2 дм-ге, ал екіншісін 4 дм-ге
қысқартты. Сонда ауданы 24 дм(2)аспайтын тіктөртбұрыш шыкты
Шаршының қабырғасы неге тең? тең?ге тең?
е)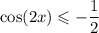
ж)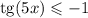
з)