Схематично построим график (см.рис.) точка имеет координаты (x;y) По графику видно, что верхняя правая вершина прямоугольника будет лежать на графике функции, если вершина будет иметь координаты (3;y) так как эта точка лежит на графике, ее координаты обращают функцию в верное равенство y=17-x²=17-3²=17-9=8
Получилась точка (3;8) -верхняя правая вершина прямоугольника
теперь найдем диагональ прямоугольника (синим цветом показана) по формуле:
одним концом диагонали является точка (-3;0) - другим (3;8)
если х₁ и х₂ корни квадратного уравнения, то по т.Виета:
{ х₁ * х₂ = -2/3
{ х₁ + х₂ = 4/3
найдем коэффициенты нового квадратного уравнения...
{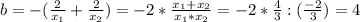
{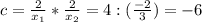
x² + 4x - 6 = 0
и можно сделать проверку:
корни получившегося уравнения D=16+24=40
х₁ = (-4-√40)/2 = -2-√10
х₂ = -2+√10
найдем корни для первого уравнения: D=16+24=40
х₁ = (4-√40)/6 = (2-√10)/3
х₂ = (2+√10)/3
-2-√10 = 2/х₁ = 2 : ((2-√10)/3) = 2*3/(2-√10) = 6*(2+√10)/(-6) = -(2+√10) верно
-2+√10 = 2/х₂ = 2 : ((2+√10)/3) = 2*3/(2+√10) = 6*(2-√10)/(-6) = -(2-√10) верно