1.
P = 2(a+b) = 26
S = ab = 42
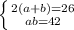
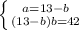
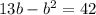
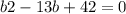
D = 1
b = 6 или b = 7
a = 7 или a = 6
ответ: 6 и 7 м.
2.
Решение данной задачи сводится к решению системы из 2х уравнений с 2мя неизвестными:
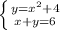
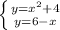
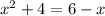
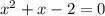
D = 9
x = -2 или x = 1
y = 6-x
y = 8 или y = 5
ответ: точки пересечения (-2;8) и (1;5)
3.
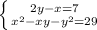
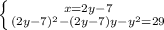
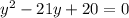
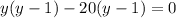
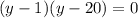
y = 1 или y = 20
x = 2y-7
x = -5 или x = 33
ответ: (-5;1) и (33;20)
4.
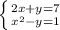
Сложим уравнения
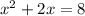
D = 36
x = -4 или x = 2
y = 7-2x
y = 15 или y = 3
ответ: (-4;15) и (2;3)
Чтобы найти вероятность, нужно количество благоприятных событий разделить на количество всех возможных событий.
Игральный кубик имеет 6 граней, значит при его бросании может выпасть либо 1, либо 2, либо 3, либо 4, либо 5, либо 6 - то есть количество всех возможных событий = 6.
По условию нам нужны только четные числа. В диапазоне от 1 до 6 всего 3 четных числа - 2, 4, 6, значит, количество благоприятных событий = 3.
Итак, количество благоприятных событий - 3, общее количество всех возможных событий - 6.
В числитель записываем благоприятные события (3), в знаменатель - все возможные события (6).
Найдем вероятность.
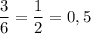 - вероятность того, что при бросании кубика Ире выпадет четное число очков.
- вероятность того, что при бросании кубика Ире выпадет четное число очков.
ответ: вероятность равна 0,5.
Объяснение:
1. а) 2х+3xу = х(2+3у)
х(2+3у) =2х+3xу
б) 3ху -5у = у(3х-5)
у (3х-5) = 3ху -5у
в) -7ху+у = у(1-7х)
у(1-7х)=-7ху+у
г) -ху-х = -х(у + 1)
-х(у + 1)=-ху-х
2. а) 5ab+10a²=5a(b+2a)
5a(b+2a) = 5ab+10a²
б) 14mn²-7n=7n(2mn-1)
7n(2mn-1)=14mn²-7n
в) -20c²+80bc= -20c(c-4b)
-20c(c-4b)=20c²+80bc
г) -3a²y-12y²=-3y(a²+4y)
-3y(a²+4y) =-3a²y-12y²
3. а) а⁴+а³=а³(а+1)
а³(а+1) = а⁴+а³
б) 2z⁵-4z³=2z³(z²-2)
2z³(z²-2) = 2z⁵-4z³
в) 3с⁶+7с⁷-8с⁸=с⁶(3+7с-8с²)
с⁶(3+7с-8с²) = 3с⁶+7с⁷-8с⁸
г) 5х²-10х³-15х⁴ = 5х²(1-2х-3х²)
5х²(1-2х-3х²) = 5х²-10х³-15х⁴
4. а) ах²+3ах=ах(х+3)
ах(х+3) = ах²+3ах
б) ху³+5х²у²-3х²у=ху(у²+5ху-3х)
ху(у²+5ху-3х)=у³+5х²у²-3х²у
в) 3а³b-6a²b²=3a²b(a-2b)
3a²b(a-2b) = 3а³b-6a²b²
г) 6c²x³-4c³x²+2c²x²=2c²x²(3x-2c+1)
2c²x²(3x-2c+1) = 6c²x³-4c³x²+2c²x²
2)
x+x2+4=6
x2+x-2=0
D=1-4*1*(-2)=9
x1=(-1+3)/2=1
x2=(-1-3)/2=-2
y1=1+4=5
y2=4+4=8
точек пересечения две:
А(1;5)
В(-2;8)
4)
y=7-2x
x^2+2x-7-1=0
x^2+2x-8=0
D=4+32=36
x1=(-2+6)/2=2
x2=(-2-6)/2=-4
y1=7-2*2=3
y2=7-2*(-4)=15