И так распишем модуль по определению.
Так программа не позволяет записывать большие уравнения буду делать по частям, а потом всё объединять.
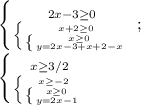
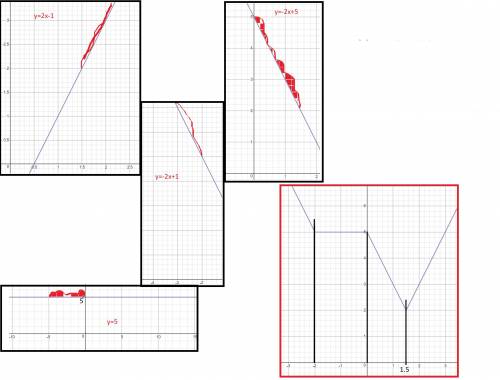
1. x≥3/2, y=2x-1
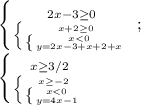
У этой системы нет пересечения.
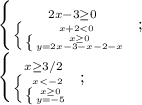
У этой системы нет пересечения.
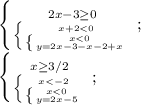
У этой системы нет пересечения.
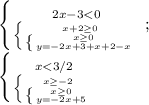
2. 0≤x<3/2, y=-2x+5
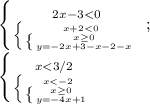
У этой системы нет пересечения.
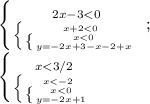
3. x<-2, y=-2x+1
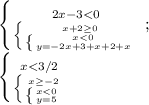
4. -2≤x<0, y=5
Я перебрал все возможные случаи раскрытия модулей теперь посмотрим прерываются ли эти графики.
1. x≥3/2, y=2x-1;
2. 0≤x<3/2, y=-2x+5;
3. x<-2, y=-2x+1;
4. -2≤x<0, y=5.
f1(3/2)=3*2/2-1=2 и f2(3/2)=-2*3/2+5= -3+5=2 Эти концы сходятся.
f2(0)= -2*0+5=5 и f4(0)=5 сходятся
f4(-2)=5 и f3(-2)= -2*(-2)+1=4+1=5 сходятся.
Далее рисуем каждый график отдельно отмечай необходимый нам интервал и переносим всё на один график. См. график внизу
Все степенные функции, а это функции вида определены на всей числовой оси, т.е. на множестве действительных чисел:
определены на всей числовой оси, т.е. на множестве действительных чисел:  . Поэтому график рисовать, чтобы определить ООФ не обязательно. Если показатель степени - нечётное число, т.е.
. Поэтому график рисовать, чтобы определить ООФ не обязательно. Если показатель степени - нечётное число, т.е.  , то все графики похожи на график функции
, то все графики похожи на график функции 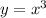 , а если показатель степени - чётное число, т.е.
, а если показатель степени - чётное число, т.е. 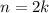 , то все графики похожи на график функции
, то все графики похожи на график функции 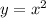 .
.
Функция чётная, если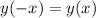 .
.
Функция нечётная, если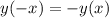 .
.