Объяснение:
простыми словами ООФ - это множество всех значений х, где функция определена и существует
в нашем случае вот какие условия:
знаменатель не может быть равен нулю
подкоренное выражение должно быть больше или равно нулю
вот и все ограничения
т.е.
5х+9-4х² >0
x-1 ≥ 0
первое условие неравенство 5х+9-4х² >0:
корни уравнения 5х+9-4х² = 0 х₁=-1, х₂ = 9/4 - точки пересечения графика с осью ОХ
поскольку это парабола ветвями вниз, то строгое неравенство выполняется на промежутке -1 < x < 9/4
теперь второе условие
x-1 ≥ 0 х ≥1
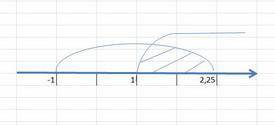
оба условия должны выполняться одновременно. объединим их и получим (чтобы нагляднее было, я нанесла все условия на чертеж и посмотрела, где они пересекаются)
1 ≤ x < 9/4
S(n) =4n² -3n. Сколько двузначных чисел есть в этой прогрессии.
ответ: 11
Объяснение:
арифметическая прогрессия: a₁=1 , d=8 ; a(n) = 1 +(n-1)8 .
10 ≤ 1 +(n-1)8 ≤ 99 ⇔ 2 1/8 ≤ n ≤ 13 1/4 ; 3 ≤ n ≤ 13
от a₃ до a₁₃ включительно, т.е. 11 членов .
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
S(n) = (2a₁+(n-1)d) *n/2 = (d/2)*n² +(a₁ -d/2)n ≡ 4n² - 3 n
{ d/2=4 ; a₁ -d/2= - 3 . ⇔ { d=8 ; a₁= 1 . ⇒ a(n)= 1 +(n-1)8
1 , 9 , 17 25, 33, 41, 49 , 57; 65 ; 73, 81, 89 , 97 , 105
1) (2х - 1)² = 2х - 1
4x² - 4x + 1 = 2x - 1
4x² - 6x + 2 = 0
или
2х² - 3х + 1 = 0
D = 9 - 8 = 1
x1 = (3 - 1)/4 = 0.5
x2 = (3 + 1)/4 = 1
2) (x - 3)² = 4(х - 3)
х² - 6х + 9 = 4х - 12
х² - 10х + 21 = 0
D = 100 - 84 = 16
x1 = (10 - 4)/2 = 3
х2 = (10 + 4)/2 = 7
3) 4(х - 3)² = (2х + 6)²
4(х - 3)² = 4(х + 3)²
(х - 3)² = (х + 3)²
х² - 6х + 9 = х² + 6х + 9
12х = 0
х = 0
4) (3х + 4)² = 3х + 4
9х² + 24х + 16 = 3х + 4
9х² + 21х + 12 = 0
D = 441 - 48 · 9 = 9
х1 = (-21 - 3)/18 = -4/3
х2 = (-21 + 3)/18 = -1