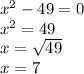 x2=-7
x2=-7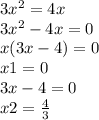
ответ:1)Алгебраической называют дробью.
2)Тождество — это уравнение, которое удовлетворяется тождественно
3)число n (показывающее сколько раз повторяется множитель) – показателем степени
4)Квадратное уравнение называют приведенным, если его старший коэффициент равен 1.
5)Решить уравнение - значит найти все его корни или установить, что их нет.
6)Деление числителя и знаменателя на их общий делитель, отличный от
единицы, называют сокращением дроби.
7)при умножении ( делении ) числителя и знаменателя на одно и то же выражение ( число) получившаяся дробь = исходной
8)числители перемножаются отдельно
отдельно знаменатели
полученную дробь если это возможно сокращают
пример
2/3* 3/4 = (2*3)/(3*4)=6/12=1/2 (произвели сокращение на 6
9)Вам известно, что значение обыкновенной дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число.
10) Сложение и вычитание алгебраических дробей c одинаковыми
знаменателями выполняется по тому же правилу, что и с обыкновенными
дробями:
аd + bd – cd = a+b−cd .
11) Нам известно, что дробь 34 равна частному 3 : 4 ,
значит, выражение ( 14+ 15) : ( 13− 16) = ( 14+ 15)( 13− 16) .
Частное двух чисел или выражений, в котором знак деления
обозначен чертой, называют дробным выражением.
Найдем значения выражений:
а) ( 14+ 15)( 13− 16) = ( 520+ 420)( 26− 16) = ( 920)( 16) = 920 : 16 =
= 920• 61 = 5420 = 2 710 = 2,7
12)Пусть a0 и a1 - натуральные числа. Для нахождения их наибольшего общего делителя используется алгоритм Евклида [1] последовательного деления с остатком: a0=a0a1+a2, a1=a1a2+a3, a2=a2a3+a4, … ,где натуральные числа a0,a1,a2, … суть неполные частные. Это алгоритм разложения числа a =a0/a1 в правильную цепную дробь, и он применим к любым вещественным числам a. При этомa0=[a], где [a] - целая часть числа a, a1=[1/(a-a0)], … , т.е.
a=a0+ 1a1+ 1a2+ 1a3+ ···,
13)http://school.xvatit.com/images/9/92/11-06-34.jpg
14)Складываются показатели степеней при УМНОЖЕНИИ степеней с одинаковыми основаниями.
2^3+2^5=8+32=40.
Подробнее - на -
Объяснение:
Если цена ресурса составляет P1, то фирма, стремясь к
получению максимальной прибыли, будет использовать Q1 единиц ресурса
(точка b). А при цене ресурса P2 фирма применяет Q2 единиц ресурса (точ-
ка a). Естественно, что фирма будет предъявлять спрос на ресурс до тех
пор, пока предельный продукт в денежном выражении (а в условиях мак-
симизации прибыли это суть цены ресурса) будет ниже среднего дохода
на единицу ресурса. Следовательно, отрезок кривой MRP, лежащий ниже
кривой ARP, и будет являться кривой спроса фирмы на ресурс.
Как видно из рис. 6.1, цене ресурса P2 соответствуют две точки на
кривой MRP (точки a и c). С точкой a мы уже определились. Что же касает-
ся точки c, то можно сказать следующее: при любом количестве единиц
ресурса, меньшем Q4, предельный продукт в денежном выражении будет
меньше цены ресурса P2, иными словами, приращение дохода фирмы, по-
лучаемое от введения дополнительной единицы ресурса, будет меньше, чем
цена ресурса. В этом случае, для фирмы, стремящейся максимизировать
прибыль, выгоднее вообще не применять данный ресурс по такой цене.
Если фирма будет использовать количество единиц ресурса больше Q4, то
каждая последующая единица ресурса явится все более выгодной для фир-
мы и максимальную прибыль фирма получит в точке a. Итак, при цене ре-
сурса P2 точка a соответствует максимальной, а точка c – минимальной
прибыли.
Сказанное выше позволяет сделать весьма важное уточнение: кривая
спроса на ресурс представляет собой нисходящую (а не восходящую!) часть
кривой MRP.
Объяснение:
а)+7,-7
б)x=0, x= 4/3