Question

Пределы найти: 1) lim x -> 0 2) lim x-> 0 3) lim x-> 0

Answer 1

Решение во вложении

Answer 2

Метод замены бесконечно малых величин эквивалентными бесконечно малыми.

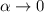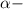( Если  $\alpha \to 0$ ,  то $\alpha -$  бесконечно малая. )

$1)\; \; \lim\limits _{x \to 0}\frac{1-sinx-cosx}{sin(\sqrt2x)}=\lim\limits _{x \to 0}\frac{1-cosx}{sin(\sqrt2x)}-\lim\limits _{x \to 0}\frac{sinx}{sin(\sqrt2x)}=\\\\=\Big [\, (1-cos\alpha )\sim \frac{\alpha ^2}{2}\; ,\; \; sin\alpha \sim \alpha \; ,\; \; \alpha \to 0\; \Big ]=\\\\=\lim\limits _{x \to 0}\frac{\frac{x^2}{2}}{\sqrt2x}-\lim\limits _{x \to 0}\frac{x}{\sqrt2x}=\lim\limits_{x \to 0}\frac{x}{2\sqrt2}-\lim\limits _{x \to 0}\frac{1}{\sqrt2}=\frac{0}{2\sqrt2}-\frac{1}{\sqrt2}=-\frac{1}{\sqrt2}$

$2)\; \; \lim\limits _{x \to 0}\frac{ln(1+x)}{x^2}=\Big [\; ln(1+\alpha )\sim \alpha \; ,esli\; \; \alpha \to 0\; \Big ]=\lim\limits _{x \to 0}\frac{x}{x^2}=\\\\=\lim\limits _{x \to 0}\frac{1}{x}=\Big [\; \frac{1}{0}\; \Big ]=\infty \\\\3)\; \; \lim\limits _{x \to 0}\frac{tgx}{2x}=\Big [\; tg\alpha \sim \alpha \; ,\; esli\; \alpha \to 0\; \Big ]=\lim\limits _{x \to 0}\frac{x}{2x}=\frac{1}{2}$