График функции y=3/x - гипербола, расположена в первой и третьей четвертях. Точки для построения :
x = 1/2; y = 3/(1/2) = 6; A(1/2; 6)
x = -1/2; y = 3/(-1/2) = -6; A'(-1/2; -6)
x = 1; y = 3/1 = 3; B(1; 3)
x = -1; y = 3/(-1) = -3; B'(-1; -3)
x = 2; y = 3/2 = 1,5; C(2; 1,5)
x = -2; y = 3/(-2) = -1,5; C'(-2; -1,5)
x = 3; y = 3/3 = 1; D(3; 1)
x = -3; y = 3/(-3) = -1; D'(-3; -1)
Область определения функции D(y) = (-∞; 0)∪(0; +∞)
Область значений функции E(y) = (-∞; 0)∪(0; +∞)
Функция убывает на всей области определения D(y) = (-∞; 0)∪(0; +∞)
Промежутки знакопостоянства :
y > 0 при x ∈ (0; +∞)
y < 0 при x ∈ (-∞; 0)
Функция нулей не имеет, пересечений с осью OY тоже.
Функция нечетная : y(-x) = 3/(-x) = -3/x = -y(x)
Функция не периодичная.
Функция имеет две асимптоты :
горизонтальную y=0 и вертикальную x=0
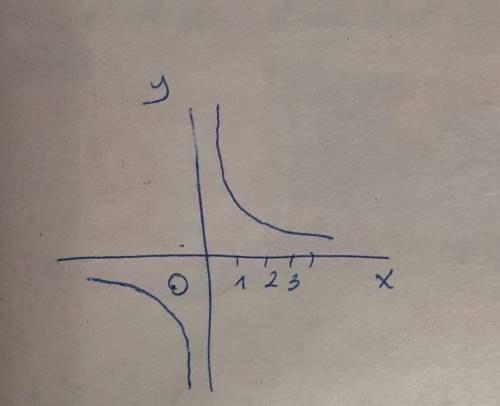
1)3^3х=3^4
3х=4
Х=4/3
Х=1. 1/3 (1целая 1/3)
2)2^2х-3*2^х-4=0
2^х=t
t^2-3t-4=0
D=9+16=25
Подкорнем25=5
t1=(3+5)/2=8/2=4
t2=(3-5)/2=-2/2=-1неудов.
2^х=4
2^х=2^2
Х=2
3)х^2+11х-3=9
Х^2+11х-3-9=0
Х^2+11х-12=0
D=121+48=169
Подкорнем169=13
Х1=(-11+13)/2=2/2=1
Х2=(-11-13)/2=-24/2=-12