Впервом баке было в 4 раза больше бензина чем во втором когда из первого бака перелить 10 л бензина во второй то оказалось что во втором баке стала 2/3 того что осталось в первом сколько литров бензина было в каждом пакете первоначально
Пусть в первом баке было бензина, а во втором — . Тогда изначально было . После переливания в первом баке осталось бензина, а во втором стало . Теперь можем составить систему уравнений:
Подставим во второе уравнение вместо :
ответ: в первом баке было 40 л, а во втором — 10 л.
Произведение двух наибольших = 225 Чтобы получить 225, можно перемножить такие разные натуральные числа: 225*1, 75*3, 45*5, 25*9.
Произведение двух наименьших = 16 Чтобы получить 16, можно перемножить такие разные натуральные числа: 16*1, 8*2.
Т.к. есть 2 самых меньших и 2 самых больших, то меньшие не могут быть больше больших (очевидно же). Поэтому есть лишь вариант 25,9 и 8,2. В любых других случаях одно из больших чисел меньше одного из меньших чисел, чего не может быть. Сумма всех чисел = 25+9+8+2 = 44
Докажем, сначала, что куб числа - монотонная функция. Монотонная функция -функций, у которой одному значению переменной соответствует только одно значение функции. Пойдем методом от противного пусть в точках х и х+с функция принимает одно и то же значение, тогда: x^3=(x+c)^3 x^3=x^3+3x^2c+3xc^2+c^3 3c *x^2+ 3c^2 *x +c^3=0|:c не равное 0 3x^2+3cx+c^2=0 D=9c^2-4*3c^2=-3c^2<0 Значит не существует такого с, что функция в при нескольких икс принимает одно и то же значение, а значит она монотонна. Если функция монотонна, то достаточно доказать, что если функция f(х+1) больше функции f(x) -то функция явл возрастающей. Пусть: (x+1)^3>x^3 x^3+3x^2+3x+1>x^3 3x^2+3x+1>0 D=9-12=-3<0 Значит уравнение корней не имеет, у параболы ветви вверх, значит она всюду больше 0 Отсюда следует, что: (x+1)^3>x^3 f(x+1)>f(x) Значит функция является монотонно возрастающей.
Пусть в первом баке было
бензина, а во втором — 
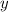. Тогда изначально было 
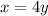. После переливания в первом баке осталось 
бензина, а во втором стало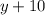 
. Теперь можем составить систему уравнений:
Подставим во второе уравнение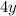
вместо 
:
ответ: в первом баке было 40 л, а во втором — 10 л.