
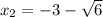
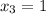

Объяснение:
(x² + 6x)² - 4(x² + 6x + 1) - 17 = 0
t = (x² + 6x)
t² - 4(t + 1) - 17 = 0
t² - 4t - 4 - 17 = 0
t² - 4t - 21 = 0
t² + 3t - 7t - 4 - 17 = 0 (Теорема Виета)
t² + 3t - 7t - 21 = 0
t(t + 3) - 7(t + 3) = 0
(t + 3)(t - 7) = 0
t₁ = -3; t₂ = 7
x² + 6x + 3= 0 x² + 6x - 7 = 0
D = b² - 4ac D = b² - 4ac
D = 6² - 4 * 1 * 3 D = 6² - 4 * 1 * (-7)
D = 36 - 12 D = 36 + 28
D = 24 D = 64
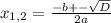



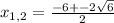

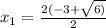

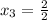
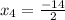

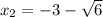
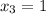

В решении.
Объяснение:
Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 3,7 км от места отправления. Один идёт со скоростью 3,3 км/ч, а другой — со скоростью 4,1 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - расстояние, которое 1 человек.
3,7 + (3,7 - х) - расстояние, которое 2 человек весь путь до опушки, 3,7 км, и вернулся часть пути (3,7 - х).
Время одно и то же в пути, уравнение:
х/3,3 = (3,7 + (3,7 - х))/4,1
х/3,3 = (7,4 - х)/4,1
4,1х = (7,4 - х)*3,3
4,1х = 24,42 - 3,3х
4,1х + 3,3х = 24,42
7,4х = 24,42
х = 24,42/7,4
х = 3,3 (км до встречи 1 человек. На этом расстоянии произошла встреча.
Проверка:
3,3/3,3 = 1 (час) - был в пути 1 человек.
(7,4 - 3,3)/4,1 = 4,1/4,1 = 1 (час) - был в пути 2 человек, верно.
6-4(3-2x)=5x-9
6-12+8x=5x-9
8x-5x=-9-6+12
-3x=-3
x=1