a = 3
Объяснение:
Имеем выражение:
a^2 - 6 * a + 11.
Необходимо найти значение аргумента a, при котором значение выражения будет минимальным.
Здесь можно приравнивать значение выражения к нулю, можно решать квадратное уравнение, можно искать значение переменной методом подбора, но единственный практичный выделить у выражения квадрат суммы или разности двух чисел:
a^2 - 6 * a + 11 = a^2 - 2 * 3 * a + 3 * 3 + 2 = (a - 3)^2 + 2.
Получили сумму квадрата числа и двойки. Наименьшее значение суммы - 2, значит, a = 3.
— угол наклона прямой, а точнее тангенс угла наклона. Так как функция убывает, то коэффициент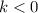 
.По клеточкам можно определить: из прямоугольного равнобедренного треугольника его углы будут равны 45°, 45° и 90°.
Так как угол развёрнутый, то угол наклона будет равен 180° - 45° = 135°.
Следовательно Тут коэффициент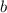 
показывает пересечение графика функции с осью ординат 
.
Из графика он равен 2.
Возьмём любую удобную точку из графика (кроме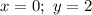 
):
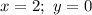
Подставим их в формулу функции и получим:
ответ: -1.
z=1/10(y-2x)
y=1/10z + 2x
x=0.5y-1/20z