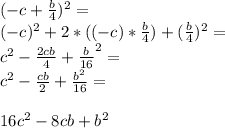Найдём уравнение плоскости АВС. Точки A(1;2;3), B(2;-1;1), C(-1;-2;0).
Вектор АВ = (1; -3; -2), вектор АС = (-2; -4; -3).
(x - 1) (y - 2) (z - 3) | (x - 1) (y - 2)
1 -3 -2 | 1 -2
-2 -4 -3 | -2 -4 = (x - 1)*9 + (y - 2)*4 + (z - 3)*(-4) - (y - 2)*(-3) - (x - 1)*8 - (z - 3)*6 = 9x - 9 + 4y - 8 - 4z + 12 + 3y - 6 - 8x + 8 - 6z +18 = x + 7y - 10z + 15 = 0.
Плоскость АВС пересекает ось Ох при значении координат y = 0, z = 0.
Отсюда координата точки на оси Ох: (-15; 0; 0).
20.000.220
Моя логика:
• число точно восьмизначное, значит, первой цифрой будет 2, чтобы очертить количество знаков
• раз число делится на круглое число (30), значит, оно должно оканчиваться на 0
• осталось только выбрать количество двоек: число, делящееся на 30, должно делиться на 3. Число делится на 3, если сумма всех его цифр делится на 3. Минимальное количество двоек в этом случае будет равно трём: 2+2+2=6, делится на 3 без остатка
• все двойки, кроме первой, расположим как можно ближе к концу, чтобы получить как можно меньшее число
1)
Это формула сокращенного умножения
Подставляем
Приводим к общему знаменателю
2)