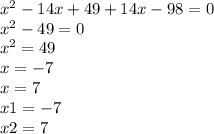
Обозначим скорость катера по течению за х км/ч. Тогда скорость катера в стоячей воде равна (х-4) км/ч. По реке катер шел 15/x часов, по стоячей воде 4/(x-4) часов.
Имеем уравнение:
15/x+4/(x-4)=1
15*(x-4)+4*x=x*(x-4)
15*x-60+4*x=x^2-4*x
Имеем квадратное уравнение:
x^2-23*x+60=0 Д=(-23)^-4*1*60=289
x1,2=23+-17 РАЗДЕЛИТЬ ВСЕ НА 2
x1=20 (км/час)
x2=3 (км/час) - посторонний корень, скорость катера по течению не может быть меньше скорости течения.
Проверка:
15/20+4/(20-4)=3/4+4/16=3/4+1/4=1 (час), что совпадает с условием задачи
ответ: Скорость катера по течению равна 20 км/x
(x-7)^2+14(x-7)=0
(x-7)(x-7+14)=0
(x-7)(x+7)=0
x=-7,
x=7
ответ: {-7; 7}