20 дней и 30 дней.
Объяснение:
Пусть один из сварщиков может выполнить всю работу за х дней,
тогда другой сварщик - за (25 * 2 - х) дней или (50 - х) дней.
Примем всю работу за 1, тогда производительность труда у первого сварщика равна 1/х, у второго сварщика - 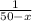 .
.
Совместна производительность труда двух сварщиков равна:
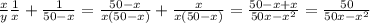
Составим уравнение и решим его:
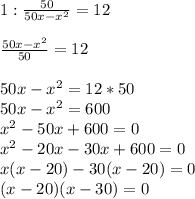
1) x - 20 = 0
x = 20 (дней)
2) x - 30 = 0
x = 30 (дней)
Допустим, что один из сварщиков может выполнить всю работу за 20 дней, тогда второй сварщик может выполнить всю работу за:
50 - 20 = 30 (дней) и наоборот.
(2x-1)²-(x-1)(x+7)≤5
4x²-4x+1-(x²+7x-x-7)-5≤0
4x²-4x+1-x²-6x+7-5≤0
3x²-10x+3≤0
D=100-36=64
x1= (10+8)/6= 3
x2= (10-8)/6= 1/3
x∈[1/3;3]