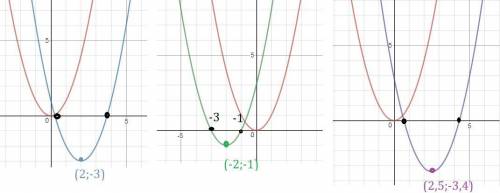
1) Шаблон y=x²
Вершина в точке (2;-3)
Нули функции
(x-2)²-3=0 ⇒
(x-2)²=3
x-2= -√3 или х-2=√3
х=2-√3 или х=2+√3
2) Шаблон y=x²
Вершина в точке (-2;-1)
Нули функции
(x+2)²-1=0 ⇒
(x+2)²=1
x+2= -1 или х+2=1
х=-3 или х=-1
3) Шаблон y=x²
Вершина в точке (2,5;-3,4)
Нули функции
(x-2,5)²-3,4=0 ⇒
(x-2,5)²=3,4
x-2,5= -√3,4 или x-2,5=√3,4
х= 2,5 -√3,4 или х=2,5 +√3,4
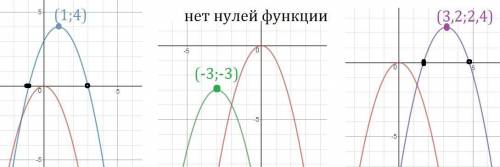
4)Шаблон y= - x²
Вершина в точке (1;4)
Нули функции
-(x-1)²+4=0 ⇒
(x-1)²=4
x-1= -2 или x-1=2
х= -1 или х=3
5)Шаблон y= - x²
Вершина в точке (-3;-3)
Нули функции
-(x+3)²-3=0 ⇒
(x+3)²=-3
уравнение не имеет корней.
Парабола не пересекает ось Ох
6)Шаблон y= - x²
Вершина в точке (3,2;2,4)
Нули функции
-(x-3,2)²+2,4=0 ⇒
(x-3,2)²=2,4
x-3,2= - √2,4 или x-3,2= √2,4
x= 3,2 - √2,4 или x = 3,2+ √2,4
ропорциональности. Приводим примеры, когда прямая пропорциональность встречается в повседневной жизни. Также на этом уроке мы строим график прямой пропорциональности и выясняем, от чего зависит расположение графика в координатной плоскости.
Конспект урока "Прямая пропорциональность и её график"
Вопросы занятия:
· ввести понятие «прямая пропорциональность»;
· привести примеры, когда прямая пропорциональность встречается в повседневной жизни;
· построить график прямой пропорциональности;
· определить от чего зависит расположение графика в координатной плоскости.
Материал урока
Давайте рассмотрим пример.
Пример.
Обратите внимание, что если переменную t увеличить, например, в 2 раза, то и переменная H также увеличится в 2 раза. То есть:
Также заметим, что зависимость высоты растения от времени его роста мы задали формулой вида:
В рассматриваемом примере: k = 2,5, а переменная t является независимой.
Сформулируем определение.
Определение.
С прямой пропорциональностью мы с вами часто встречаемся в повседневной жизни.
Например,
Или,
Теперь давайте построим график прямой пропорциональности:
Видим, что все точки лежат на одной прямой, которая проходит через начало координат. Для убедительности можем даже приложить линейку.
Таким образом, можем сформулировать определение.
Определение.
Графиком прямой пропорциональности y = kx является прямая, проходящая через начало координат.
Нам известно, что прямая определяется двумя точками. А значит, для построения графика функции y = kx достаточно указать любую точку графика этой функции, которая отличается от точки с координатами: (0, 0), то есть от начала координат.
Например,
А теперь посмотрите на рисунок, на котором изображены графики прямой пропорциональности.
Обратите внимание, что графики тех функций, которые имеют положительный коэффициент k расположены в первой и третьей координатных четвертях, а которые имеют отрицательный коэффициент k – во второй и четвёртой четвертях. То есть расположение графика функции y = kx в координатной плоскости зависит от коэффициента k.
32-2x2>0⇒2 (4-x) (x+4) >0⇒-4
6-x>0⇒x<6
x+5>0⇒x>-5
x∈ (-4;4)
log (3) (32-2x2) - log (3) (6-x) - log (3) (x+5) = 0
log (3) (32-2x2) / (6-x) (x+5) = 0
(32-2x2) / (6-x) (x+5) = 1
32-2x2 = (6-x) (x+5)
6x+30-x2-5x-32+2x2=0
x2+x-2=0
x1+x2=-1 U x1*x2=-2
x1=-2 U x2=1
2) ОДз
8-x>0⇒x<8
32-4x>0⇒4x<32⇒x<8
x+4>0⇒x>-4
x∈ (-4;8)
lg (32-4x) - lg (x+4) - lg (8-x) = 0
lg4 (8-x) / (8-x) (x+4) = 0
4 / (x+4) = 1
x+4=4
x=4-4
x=0