Question

Дан треугольник авс с координатами а(6; 3) в(5; -2) с(-5; 2) найти: 1) скалярное произведение векторов (ав*ас) 2) угол а 3) координаты точек пересечения медиан 4) длину высоты,опущенной из точки а 5) площадь треугольника авс

Answer 1

Расстояние между 2мя точками находится по формуле:
$S=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$ 

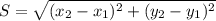
Используя эту формулу, найдем длины сторон треугольника ABC:

$AB=\sqrt{26}$

$BC=2\sqrt{29}$

$AC=\sqrt{122}$

1) Скалярное поизведение векторов равно произведению их модулей на косинус угла между ними. Отсюда:

$(AB*AC)=|AB|*|AC|cos\alpha$

Для его нахождения требуется найти cos(a). Найдем его по теореме косинусов:

BC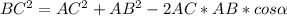$BC^2=AC^2+AB^2-2AC*AB*cos\alpha$

Отсюда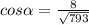 $cos\alpha=\frac{8}{\sqrt{793}}$

Подставим в ур-е и найдем скалярное поизведение векторов:

(AB*AC)=16

2) Т.к.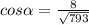 $cos\alpha=\frac{8}{\sqrt{793}}$, => угол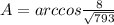 $A=arccos\frac{8}{\sqrt{793}}$

3)---

4)---

5) По формуле Герона площадь треугольника равна:
$S=\sqrt{p(p-AB)(p-BC)(p-AC)}$ 

$p=\frac{AB+BC+AC}{2}$

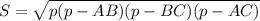
Отсюда можно найти площадь.