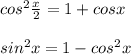
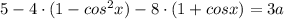
Получаем квадратное уравнение относительно
cosx=t
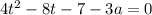
Это уравнение имеет хотя бы один корень, если D ≥0
D=64+16(7+3a)=16(11+3a)
D≥0⇒ 11+3a≥0⇒ a≥ -11/3
t₁=1- (√(11+3а))/2 или t₂=1+ (√(11+3а))/2
Обратная замена приводит к уравнениям вида cos=t₁ или cosx=t₂
Чтобы эти уравнения имели хотя бы один корень, необходимо, что бы
-1 ≤ t₁ ≤1 или -1 ≤ t₂ ≤1
Решаем неравенства:
-1 ≤1+ (√(11+3а))/2 ≤1
-2≤√(11+3а))/2≤0
-4≤√(11+3а)≤0
Решением неравенства является
11+3a=0
a=-11/3
t₁=t₂=1/2
cosx=1/2
x=±(π/3)+2πn, n∈Z
Неравенство
-1 ≤1- (√(11+3а))/2 ≤1
также приводит к ответу a=-11/3
О т в е т. При а=-11/3
x=±(π/3)+2πn, n∈Z
1-й случай.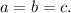
Разделив уравнение на 
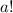, получаем 
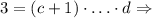в правой части на самом деле один множитель; 
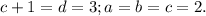Проверка: 
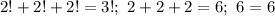- верно. Итак, одно решение найдено.
2-й случай.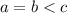
. Разделив уравнение на 
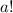, получаем 
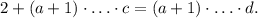Следовательно, 
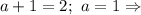уравнение имеет вид 
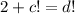Но два факториала не могут отличаться на 2, поэтому в этом случае уравнение решений не имеет.
3-й случай.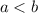
. Разделив уравнение на 
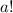, получаем 
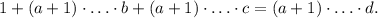Такое уравнение не может иметь решений, так как все слагаемые, кроме первого, делятся на a+1.
ответ: a=b=c=2; d=3